المعايير القياسية
معايير المتجهات
معايير المتجهات هي دوال رياضية تُستخدم لقياس طول أو حجم المتجه في الفضاء، أي لتحديد "كبره" بغض النظر عن اتجاهه. وتُعد هذه المعايير أدوات أساسية في عدة مجالات مثل الرياضيات، وعلوم الحاسوب، والذكاء الاصطناعي، وتحليل البيانات، حيث تُستخدم لقياس الأخطاء، وتحديث الأوزان، وفرض القيود في مسائل التحسين، إضافة إلى تحديد التشابه أو المسافات بين النقاط في تحليل البيانات، وفهم استقرارية العمليات في الجبر الخطي.
من أشهر هذه المعايير: المعيار الأول، ويُعرف بمعيار مانهاتن، ويُحسب بجمع القيم المطلقة لمكونات المتجه؛
المعيار الثاني، وهو المعيار الإقليدي، ويُحسب بجذر مجموع مربعات المكونات؛
والمعيار اللانهائي، الذي يُحسب بأخذ أكبر قيمة مطلقة (أو القيمة العُظمى) بين مكونات المتجه.
هذه المعايير جميعها تُعد حالات خاصة من ما يُعرف بالمعيار من الدرجة، ويُعرّف رياضيًا كالتالي:
حيث د عدد حقيقي موجب. عند اختيار د = 1 ، نحصل على معيار مانهاتن، وعند د = 2 ، نحصل على المعيار الإقليدي. يمكن اعتبار هذه المعايير جزءًا من سلسلة مستمرة من المعايير التي تزداد دقتها في تتبّع أكبر مكوّن في المتجه كلما كبر . فكلما ارتفعت قيمة ، زاد تأثير المكوّنات الأكبر للمتجه على قيمة المعيار، لأن الأس الأكبر يُضخّم الفروقات بين القيم. و منه عند اقتراب من اللانهاية، يصبح تأثير أصغر المكونات مهملًا تمامًا، ويصبح المعيار مساويًا لأكبر قيمة مطلقة بين مكونات المتجه فبالتالي، يمكن القول إن المعيار اللانهائي هو نهاية المعايير عندما يقترب من ما لا نهاية. هذا الرابط بين المعايير يعكس تطورًا تدريجيًا في طبيعة القياس: من احتساب المجموع الكلي للقيم إلى التركيز فقط على المكوّن الأعظم.
توحيد المتجهات
عند توحيد المتجهات، أي عند قسمة كل متجه على طوله بحسب أحد هذه المعايير، نحصل على متجه جديد يشير في نفس الاتجاه، لكن طوله يصبح مساويًا لـ 1 بالنسبة للمعيار المستخدم، وليس بالنسبة لبقية المعايير. وهذا ما يجعل التوحيد مرتبطًا ارتباطًا وثيقًا بالمفهوم الهندسي للمعيار ذاته.
فعند رسم رؤوس جميع هذه المتجهات الموحدة في الفضاء الثنائي الأبعاد (على سبيل المثال)، تتكوّن أشكال هندسية تختلف باختلاف المعيار المُستخدم. فإذا استخدمنا المعيار الإقليدي، نحصل على دائرة نصف قطرها واحد تُعرف باسم "دائرة الوحدة". أما في حالة معيار مانهاتن، نحصل على شكل مُعيّن، في حين أن المعيار اللانهائي يؤدي إلى شكل مربع. وكلما زادت رتبة ، اقترب شكل "دائرة الوحدة" من المربع.
عند الاقتراب من القيم التي تقل عن الواحد (أي عندما تقترب رتبة المعيار من الصفر)، يبدأ شكل "دائرة الوحدة" في التحول بشكل ملحوظ. في هذه الحالة، تتركز معظم الكتلة حول المحاور، ويصبح الشكل أكثر انكماشًا نحو زوايا المحاور، مما يعني أن المتجهات الموحدة تميل لأن تكون أكثر تركيزًا على الاتجاهات الأساسية (المحاور نفسها).
عندما تقترب الرتبة من الصفر، يصبح الشكل أقرب ما يمكن إلى مجموعة من النقاط عند رؤوس المحاور، مما يعكس أن المعيار في هذه الحالة يعطي وزنًا أكبر للقيم القريبة من الصفر على حساب القيم الكبيرة. يمكن تصور ذلك على أنه نوع من "الانهيار" إلى الاتجاهات الأساسية، حيث تفقد الوحدة شكلها الدائري أو المحدب التقليدي وتتحول إلى هيكل يقتصر تقريبًا على المحاور فقط.
هذا يبرز الجانب الهندسي الغريب للمعايير ذات الرتب الصغيرة، حيث تتلاشى فكرة "الكرة" أو "الدائرة" التقليدية تمامًا، وتعكس بدلاً من ذلك التركيز على عناصر محددة للغاية في الفضاء.
في الفضاء ثلاثي الأبعاد، يؤدي توحيد المتجهات إلى أشكال هندسية تختلف بحسب المعيار المستخدم. فعند تقسيم كل متجه على طوله وفقًا لأحد المعايير، نحصل على متجه جديد بنفس الاتجاه ولكن بطول يساوي واحد.
في حالة المعيار الإقليدي، تكون النتيجة كرة الوحدة، حيث جميع النقاط على سطحها تبعد مسافة ثابتة (تساوي واحد) عن المركز. هذه الكرة تمثل جميع المتجهات الموحدة وفقًا لهذا المعيار.
أما إذا استخدمنا معيار مانهاتن، نحصل على مجسم ثماني الأوجه مركزه الأصل، حيث يكون مجموع القيم المطلقة للإحداثيات يساوي واحد. هذا الشكل يعكس طبيعة المسافة التي تقيس المسافة كجمع للإزاحات في كل محور.
عند استخدام المعيار اللانهائي، نحصل على مكعب الوحدة الذي تساوي أطوال أضلاعه اثنين، حيث يكون مركزه عند الأصل وطول نصف ضلعه واحد. يظهر هذا الشكل لأن المعيار يعتمد على أكبر قيمة مطلقة للإحداثيات.
بين هذه المعايير، يؤدي استخدام معيار من رتبة وسيطة إلى أشكال تتغير تدريجيًا من الكرة المثالية إلى المكعب الحاد الأطراف، مما يبرز العلاقة الجمالية بين المعايير. فكلما زادت الرتبة، اقترب الشكل من المكعب، وكلما انخفضت، اقترب من المجسم ثماني الأوجه.
لا يقتصر هذا المفهوم على الفضاءات ثنائية الأبعاد أو ثلاثية الأبعاد فقط، بل يمتد إلى الفضاءات ذات الأبعاد الأعلى، حيث تتخذ الأشكال الموحدة تكوينات هندسية معقدة تتكيف مع طبيعة المعيار المختار.
معايير المصفوفات
عند حساب معايير المصفوفات، يمكن توسيع مفهوم المعايير من المتجهات إلى المصفوفات عبر التعامل مع الصفوف أو الأعمدة كمتجهات فرعية. هناك طريقتان شائعتان لحساب معيار المصفوفة بناءً على معايير الصفوف أو الأعمدة:
- معيار صفوفي: يتم أولاً حساب معيار كل صف (مثلاً باستخدام المعيار الإقليدي أو مانهاتن)، ثم يتم تجميع هذه المعايير باستخدام معيار آخر (عادة المعيار الأعظمي) لحساب المعيار النهائي.
- معيار عمودي: مشابه للطريقة الصفوفية، ولكن يتم حساب معيار كل عمود أولاً، ثم تجميع هذه المعايير باستخدام معيار آخر.
أمثلة
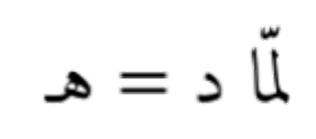 ←
←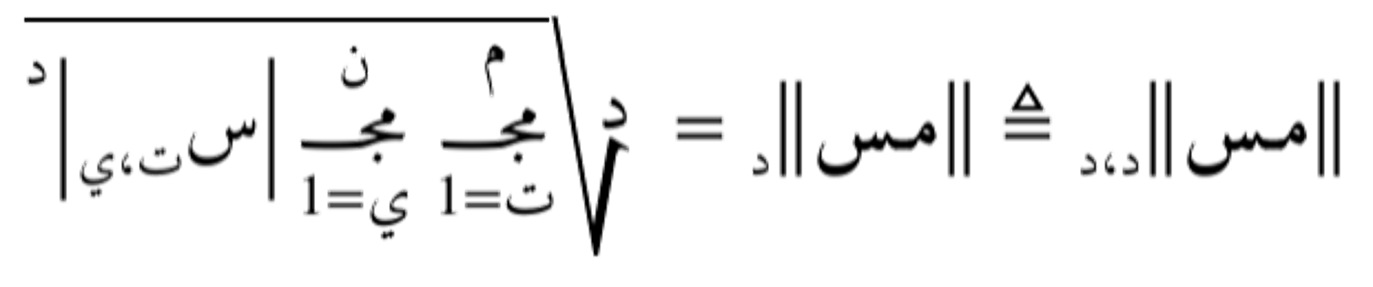
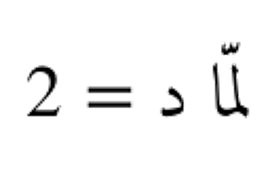 ←
←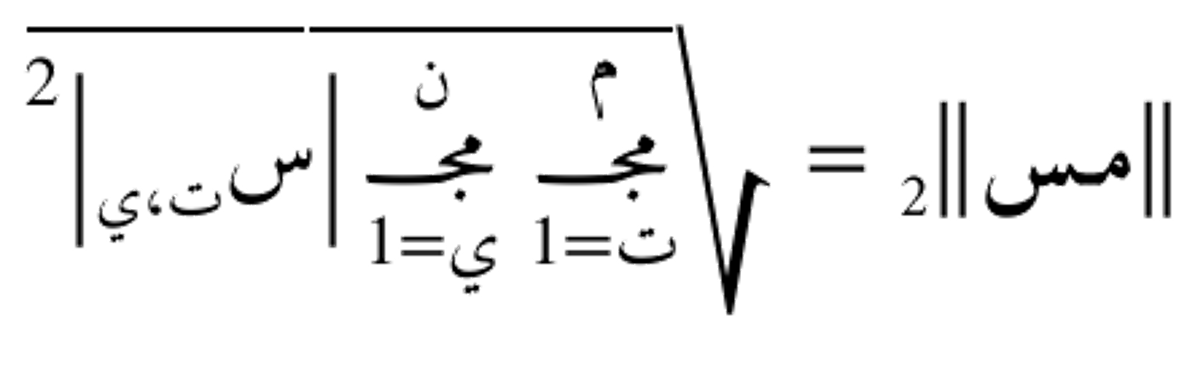
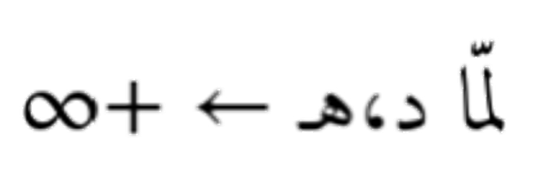 ←
←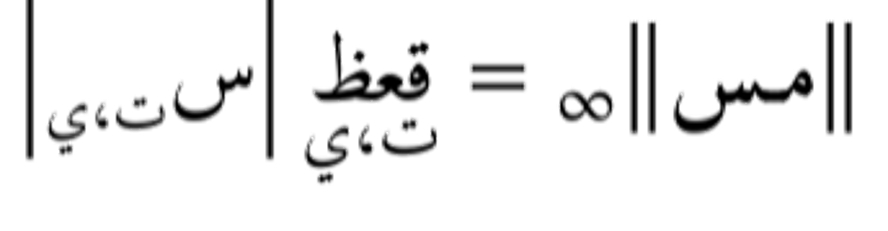
الامتداد إلى الموترات
يمكن أيضًا تمديد هذا المفهوم إلى الموترات، وهي كائنات رياضية ذات أبعاد أعلى من المصفوفات. يمكن حساب معيار الموتر عبر التعامل مع كل بعد على حدة، مثل حساب معايير الألياف (امتداد الصفوف أو الأعمدة في الأبعاد الأعلى)، ثم تجميع هذه المعايير باستخدام معيار إضافي.
بهذا الشكل، يمكن استخدام نفس الفكرة المطبقة على المتجهات والمصفوفات، ولكن بشكل متكرر على جميع الأبعاد، مما ينتج معيارًا موحدًا للموتر يأخذ في الاعتبار جميع مكوناته.






