۞
✵
۞
◉✵◉
→السابق
✦
تحليل القيمة المنفردة
۩
◉
۩

الموترات

الموترات

الموترات هي كائنات رياضية تُستخدم لوصف البيانات في عدة أبعاد. يمكن اعتبارها تعميمًا للمتجهات والمصفوفات، حيث يمكن أن تكون منعدمة البعد (عدد)، أحادية البُعد (متجه)، ثنائية البُعد (مصفوفة)، أو متعددة الأبعاد (موتر ثلاثي الأبعاد، رباعي الأبعاد، إلخ). تُستخدم الموترات في مجالات متعددة مثل الفيزياء، علوم الحاسوب، والتعلم الآلي.

الترميز الشائع للموترات

  • عدد: م
  • متجه: س
  • مصفوفة: مـس
  • موتر ثلاثي الأبعاد: موس
  • موتر رباعي الأبعاد: موس

ملاحظة عامة: عند الحديث عن المصفوفات أو الموترات بشكل عام، يمكن استخدام رموز مختلفة حسب اسم الكائن. فمثلاً، إذا كانت المصفوفة اسمها ص نكتب مـص، أو إذا كان اسم الموتر هو س نكتب موس، وهكذا.

ملاحظة: للوصول إلى عنصر محدد داخل الموتر، يُستخدم الترميز مثلمتجهللمتجه،متجهللمصفوفة،متجهللموتر ثلاثي الأبعاد، ومتجهللموتر رباعي الأبعاد حسب مؤشر العنصر ذاته.

نقل الموترات

نقل الموترات هو عملية رياضية تُستخدم لتغيير ترتيب العناصر داخل الموتر. هذه العملية تُعتبر مهمة في العديد من التطبيقات الرياضية والهندسية، حيث تساعد في إعادة ترتيب البيانات أو تغيير شكل الموتر دون فقدان المعلومات.

عند نقل موتر عددي (عدد)، يبقى كما هو لأنّ لا يوجد موضع آخر لنقلِه إليه. أما بالنسبة للمتجهات، فإن نقل متجه صف يحوله إلى متجه عمود، والعكس صحيح، أي يتم تبديل اتجاه المتجه. بالنسبة للمصفوفات، فإن عملية النقل تعني تبديل الصفوف مع الأعمدة، بحيث يصبح العنصر في الصف ي والعمود ت في الموضع ت وي بعد النقل.

بشكل عام، نقل الموترات ذات الأبعاد الأعلى (ثلاثية أو رباعية الأبعاد) يعني تبديل ترتيب المحاور أو المؤشرات الخاصة بها. على سبيل المثال، في موتر ثلاثي الأبعاد، يمكن نقل المحور الأول مع الثاني أو الثالث، مما يؤدي إلى إعادة ترتيب البيانات داخل الموتر. هذه العمليات مهمة في العديد من التطبيقات مثل معالجة الصور، التعلم العميق، وتحليل البيانات متعددة الأبعاد.

الترميز الشائع لنقل (تبديل) الموترات

🔷 مثال على نقل موتر ثلاثي الأبعاد

لنفترض أن لدينا موترًا ثلاثي الأبعاد: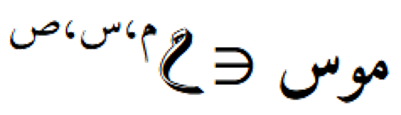متجه

  • تبديل المحور الأول والثاني:
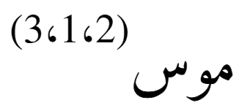    متجهأيمتجه
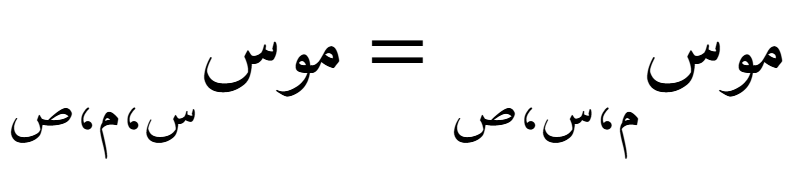
  • إعادة ترتيب المحاور إلى (ص،س،م):
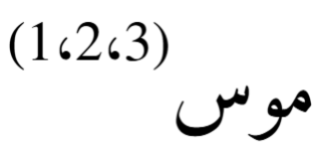    متجهأيمتجه

🔷 مثال على نقل موتر رباعي الأبعاد

لنفترض:متجه

  • تبديل المحور الأول والثاني:
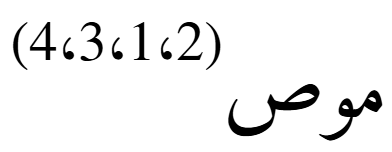    متجهأيمتجه
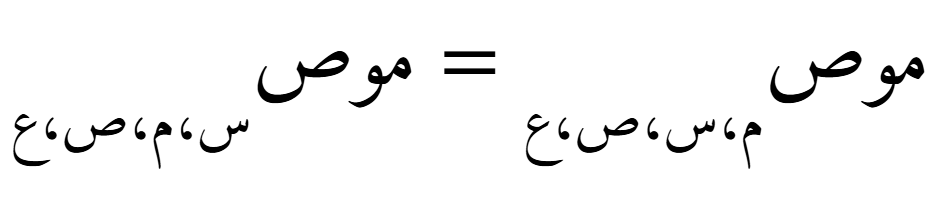
  • نقل المحور الأخير إلى البداية:
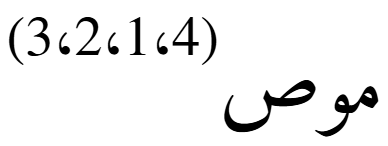    متجهأيمتجه

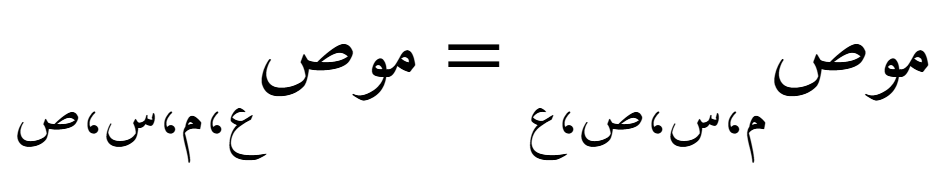
🔷 ملخص سريع

الشكل الأصليالترتيب الجديدالشكل الناتجالوصف
(م، س، ص)(2، 1، 3)(س، م، ص)تبديل المحورين الأول والثاني
(م، س، ص)(3، 2، 1)(ص، س، م)عكس ترتيب المحاور
(م، س، ص، ع)(2، 1، 3، 4)(س، م، ص، ع)تبديل المحورين الأول والثاني
(م، س، ص، ع)(4، 1، 2، 3)(ع، م، س، ص)نقل المحور الأخير إلى البداية

ملاحظة: نقل الموترات في الأبعاد العليا يعني فقط إعادة ترتيب المحاور (المؤشرات) حسب الحاجة، سواء رياضيًا أو برمجيًا.

موترات ثلاثية الأبعاد

موتر ذات بُعد [4،3،2]

موترات رباعية الأبعاد

موتر ذات بُعد [2،4،3،2]

ضرب الموترات

يتم ضرب الموترات عن طريق ضرب عناصرها وفقًا لقواعد معينة، وذلك حسب نوع الموترات وأبعادها.

ضرب الموترات أحادية البُعد (المتجهات)

ضرب المتجهات يمكن أن يكون ضربًا داخليًا أو ضربًا خارجيًا. الضرب الداخلي ينتج عددًا عبر ضرب العناصر المقابلة وجمعها. الضرب الخارجي ينتج مصفوفة ثنائية الأبعاد، حيث كل عنصر فيها هو حاصل ضرب عنصر من المتجه الأول مع عنصر من المتجه الثاني.

ضرب الموترات ثنائية البُعد (المصفوفات)

ضرب المصفوفات يتم عبر ضرب الصفوف في الأعمدة. إذا كانت المصفوفتان س و ص، فإن العنصر الناتج في الموضع (ت، ي) في المصفوفة الناتجة هو حاصل ضرب الصف ت من س في العمود ي من ص.

ضرب الموترات متعددة الأبعاد

ضرب الموترات متعددة الأبعاد يعتمد على ترتيب أو اختيار المحاور التي سيتم إجراء الضرب عليها. يمكن ضرب موتر ثلاثي الأبعاد بموتر آخر ثلاثي أو رباعي الأبعاد، ولكن يجب أن يكون هناك توافق في الأبعاد على المحاور المختارة. يتم ضرب العناصر المقابلة وجمعها حسب ترتيب أو اختيار هذه المحاور.

الموترات ثلاثية الأبعاد

في هذا المثال، يتم ضرب موتر ثلاثي الأبعاد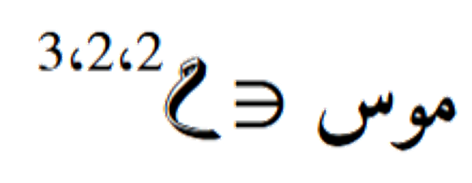متجهبموتر آخر ثنائي البُعدين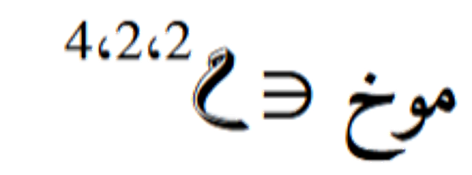متجه. يتم تحديد المحاور التي سيتم ضربها بناءً على ترتيبها في الموترات. النتيجة ستكون موترًا جديدًا بأبعاد مختلفة حسب المحاور المختارة. في هذه الحالة يوجد إمكانية ضرب واحدة متاحة وهي ضرب المحور الثالث للموتر مع المحور الثاني للمصفوفة. الناتج أيضا موتر ثلاثي الأبعادمتجه.

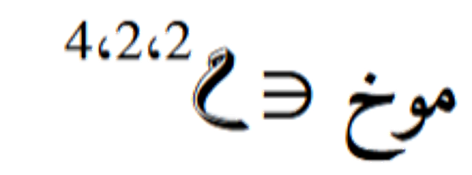الموترات رباعية الأبعاد

في هذا المثال، يتم ضرب موتر ثلاثي الأبعاد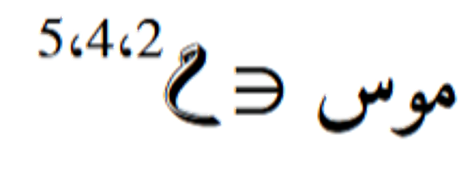متجهبموتر ثلاثي الأبعاد آخر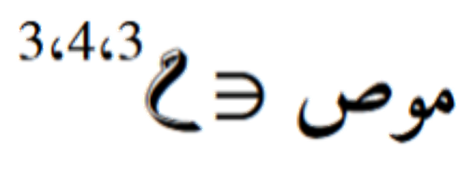متجه. يتم تحديد المحاور التي سيتم ضربها بناءً على ترتيبها في الموترات. النتيجة ستكون موترًا رباعي الأبعاد بأبعاد مختلفة حسب المحاور المختارة وهي المحوريين الثانيين للكلّ موترمتجه.

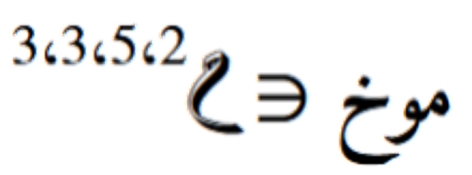معايير الموترات

المصفوفات

في الموترات ثنائية البُعد (المصفوفات)، يمكن حساب معيار الموتر باستخدام معايير الصفوف والأعمدة. يتم حساب معيار الموتر من خلال أخذ الجذر التربيعي لمجموع مربعات عناصر الموتر، سواءً كان ذلك عبر الصفوف أو الأعمدة.

الموترات

ينطبق هذا المفهوم على جميع الموترات متعددة الأبعاد بشكل عام، وليس فقط على الموترات رباعية الأبعاد؛ حيث تم ذكر الموتر رباعي الأبعاد هنا كمثال توضيحي. حساب المعيار يعتمد على اعتبار الموتر كمجموعة من المتجهات عبر محور معين (أي تحديد محور كـ"بعد متجه")، إذن ترتيب المحاور مهمّ لأن النتيجة ستعتمد على كيفية تقسيم الأبعاد.

الموترات رباعية الأبعاد

۞
✵
۞
◉✵◉
→السابق
✦
تحليل القيمة المنفردة
۩
◉
۩