تحليل القيمة المنفردة
مقدمة
تحليل القيمة المنفردة هو تقنية رياضية تُستخدم لتحليل المصفوفات. يُعتبر تحليل القيمة المنفردة أداة قوية في العديد من المجالات، بما في ذلك معالجة الصور، وتقليل الأبعاد، والتعلم الآلي.
في هذا الدرس، سوف نستعرض مفهوم تحليل القيمة المنفردة، وكيفية حسابه، وتطبيقاته العملية.
العلاقة مع تحليل القيم الذاتية
تحليل القيمة المنفردة يُعتبر تعميماً لتحليل القيم الذاتية للمصفوفات. بينما تحليل القيم الذاتية يُطبّق فقط على المصفوفات المربعة، فإن تحليل القيمة المنفردة يمكن تطبيقه على أي مصفوفة مستطيلة أو مربعة.
مصفوفة القِيَم المُنفردة
تذكير حول رُتب المصفوفات
نعرّف قذ أنها القيم الذاتية للمصفوفة المربّعة. ومنه جذور القيم الذاتية هاته هي القيم المنفردة قف للمصفوفة المستطيلة الأصلية.
نبني مصفوفة القيم المنفردة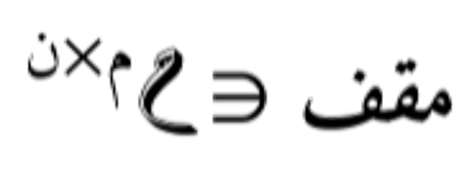
من خلال أخذ الجذور التربيعية للقيم الذاتية قذ أعلاه.
مع إمكانية ر = ن إذا كانت المصفوفة ذات رُتبة كاملة في حالة ن < م (مصفوفة طويلة) و ر = م في حالة ن > م (مصفوفة عريضة ذات رتبة كاملة أيضاً).
مصفوفات المُتجهات المُنفردة
تحليل القيمة المنفردة يُعطي أيضاً متجهات منفردة، وهي متجهات خاصة ترتبط بالقيم المنفردة. هذه المتجهات تُستخدم لوصف بنية المصفوفة.
هناك نوعان من المتجهات المنفردة: متجهات منفردة يمينية (أعمدة المصفوفة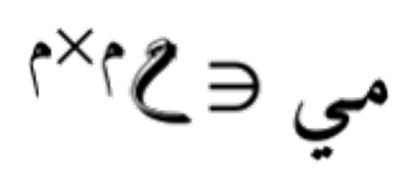
) ومتجهات منفردة شمالية (أعمدة المصفوفة
). المتجهات المنفردة اليمينية ترتبط بفضاء الإدخال، بينما المتجهات المنفردة الشمالية ترتبط بفضاء الإخراج للمصفوفة.
السبب في ظهور متجهات منفردة يمينية وشمالية هو أن المصفوفة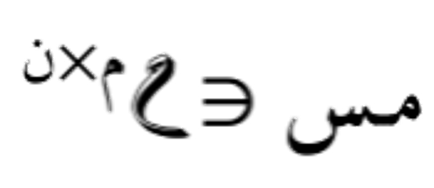
مستطيلة وليست مربعة كما في تحليل القيم الذاتية، ولذلك نحتاج إلى مجموعتين من المتجهات لوصف فضاءي الإدخال والإخراج بشكل منفصل.
المتجهات المنفردة اليمينية
نجد المتجهات اليمينية بحلّ المعادلة التالية:
لنحصل على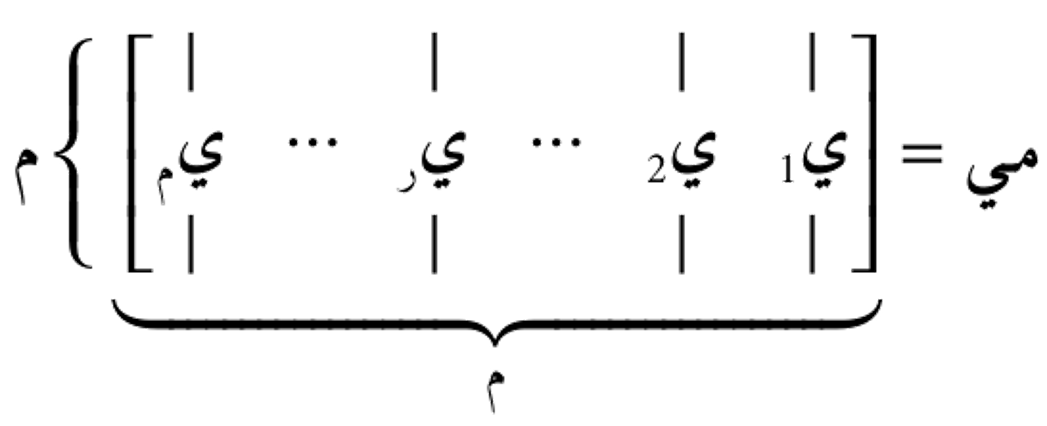
المتجهات المنفردة الشِمالية
نجد المتجهات الشِمالية بحلّ المعادلة التالية:
لنحصل على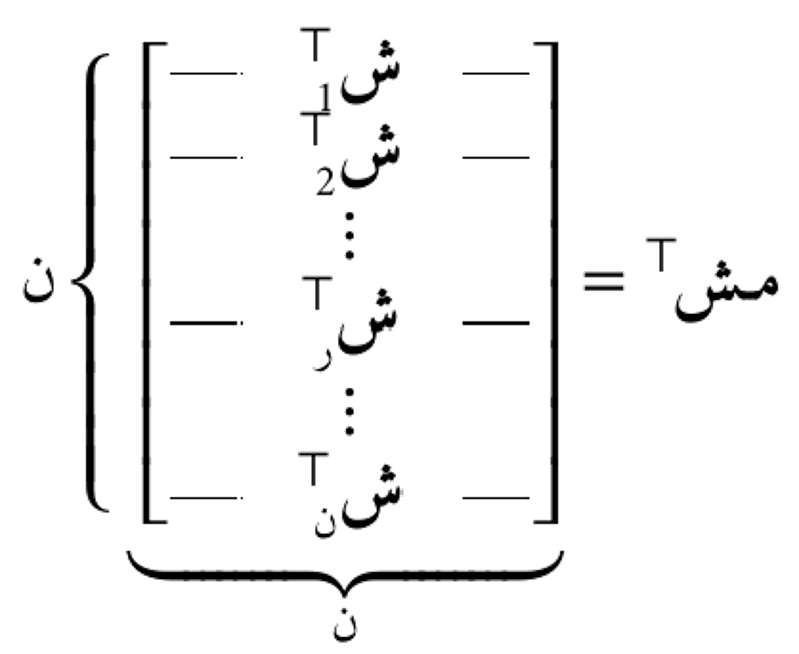
تحليل القيمة المنفردة
يمك إذن كتابة المصفوفة مـس على صورة: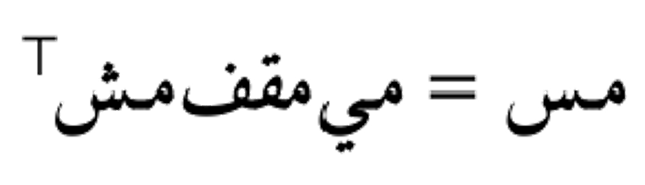
القيم المنفردة هي قيم غير سالبة، وتُرتب عادةً من الأكبر إلى الأصغر. هذه القيم تعطي معلومات حول مدى أهمية كل بُعد في المصفوفة. القيم المنفردة الكبيرة تشير إلى أبعاد مهمة في البيانات، بينما القيم الصغيرة تشير إلى أبعاد أقل أهمية.
التقريب بقَطع القيم المنفردة
من التطبيقات المهمة لتحليل القيمة المنفردة هو تقريب المصفوفات. يمكننا الحصول على تقريب جيد للمصفوفة الأصلية من خلال الاحتفاظ بعدد قليل فقط من أكبر القيم المنفردة، وتجاهل القيم الصغيرة (القَطع).
هذا يعني أننا نستبدل المصفوفة الأصلية بمصفوفة رتبتها أقل، لكنها تحتفظ بمعظم المعلومات الأساسية. هذه الطريقة تُستخدم كثيراً في ضغط الصور والبيانات، حيث يمكن تمثيل البيانات بدقة عالية باستخدام عدد أقل من الأبعاد.
تطبيقات ضغط الصور غير المربعة وتجميع الصور
تحليل القيمة المنفردة يُستخدم بكفاءة في ضغط الصور، حتى لو لم تكن الصور مربعة. يمكن تمثيل أي صورة (مستطيلة أو مربعة) كمصفوفة، وتطبيق التحليل عليها للحصول على تقريب منخفض الرتبة يحافظ على معظم التفاصيل مع تقليل حجم البيانات.
أيضاً عند التعامل مع مجموعة من الصور، يمكن ضغطها معًا بدمج كل صورة في متجه (عن طريق تسطيحها صفاً بعد صف أي إعادة تشكيلها)، ثم تجميع هذه المتجهات في مصفوفة كبيرة (طويلة أو عريضة حسب عدد الصور وحجم كل صورة). بعد ذلك، نطبّق التحليل على هذه المصفوفة للحصول على تمثيل مضغوط مشترك للصور جميعها.
خلاصة
- في تحليل القيم الذاتية، نبحث عن متجهات وقيم تحقق مـس س = م س حيث مـس مصفوفة مربعة.
- في تحليل القيم الذاتية، يمكننا كتابة مصفوفة مربعة مـس على صورة Tممذ مقذ ممذ حيث ممذ مصفوفة أعمدتها هي المتجهات الذاتية و مصفوفة قطرية تحتوي على القيم الذاتية.
- في تحليل القيمة المنفردة، يمكننا كتابة أي مصفوفة مـس كـ Tمـس = مي مقف مش حيث مش و مي مصفوفتان متعامدتان و مقف مصفوفة قطرية.
- القيم المنفردة في مقف هي الجذور التربيعية للقيم الذاتية للمصفوفة مـسTمـس أو Tمـس مـس.
بذلك، يُمكن اعتبار تحليل القيمة المنفردة امتداداً لتحليل القيم الذاتية ليشمل جميع أنواع المصفوفات، ويوفّر معلومات أكثر حول بنية المصفوفة.