عمليات على الدوّال
عمليات على الدوّال
في هذا الدرس، سوف نتناول العمليات الأساسية التي يمكن إجراؤها على الدوّال. هذه العمليات تشمل الجمع والطرح والضرب والقسمة، وهي تشكل الأساس لفهم كيفية التعامل مع الدوّال في الرياضيات.
الدوّال هي تعبيرات رياضية تربط بين متغيرين أو أكثر، ويمكن أن تكون خطية أو غير خطية. العمليات على الدوّال تسمح لنا بإنشاء دوّال جديدة من دوّال موجودة، مما يتيح لنا تحليل العلاقات الرياضية بشكل أعمق.
في هذا الصفحة سنستعرض بعض الأمثلة لهذه العمليات على الدوّال. الهدف هو فهم استخدام هذه العمليات في سياقات مختلفة
المثال الأوّل
من أشهر العلاقات في الدوال المثلثية هي العلاقة التالية: جتا²(س) + جا²(س) = 1
هذه العلاقة تُسمّى المُتطابقة المثلثية الأساسية، وتُستخدم كثيرًا في تبسيط وحل المسائل الرياضية التي تتعلق بالدوّال المثلثية. نلاحظ في الرسوم المتحركة أسفله كيف الدالتين الجيبيتين تتغيّر أوّلا لوحدهما قبل أنّ ننظر إلى تطوّر المجموع مربّعيهما كما في المتطابقة الأساسية المذكورة أعلاه.
المثال الثاني
في هذا المثال، نستعرض كيف يمكن أن تؤثر دالة دورية على سلوك دالة أخرى، مثل الدالة التربيعية. عند دمج الدالة التربيعية مع دالة دورية، نحصل على دالة جديدة تجمع بين الطابع التذبذبي للدالة الدورية والشكل العام للدالة التربيعية، كما يظهر في الرسم أدناه.
المثال الثالث
في هذا المثال، نستعرض الدالة التخميدية، وهي دالة تجمع بين دالة أسية تنازلية ودالة دورية مثل الجيب أو الجيب تمام. هذا النوع من الدوال يُستخدم لوصف الظواهر التي تبدأ بتذبذب ثم يقل سعتها تدريجيًا مع الزمن، مثل اهتزاز نابض أو تلاشي موجة كهربائية.
نلاحظ في الرسم كيف أن سعة التذبذب تتناقص تدريجيًا مع الزمن نتيجة تأثير الدالة الأسية، بينما يستمر التذبذب بفعل الدالة الدورية.
تركيب الدوالّ
تركيب الدوالّ هو عملية إنشاء دالة جديدة من خلال تطبيق دالتين على بعضها البعض. إذا كانت لدينا دالتان د(س) و ل(س)، فإن تركيب الدالتين يُكتب كالتالي حسب ترتيب التطبيق: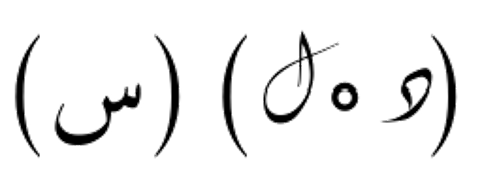
.
مثال على تركيب الدوالّ
نأخد الدالة الأولى والتي هي أصلا مكوّنة من دالتين مضروبتين فيما بعض. الدالة الجيبية مضروبة في الدالة الخطية حيث أن نلاحظ كما في رسم الدالة أسفله أن سعة الذبذب تتغيّر خطيا.
ثم نأخد الدالة الثانية والتي هي فقط الدالة التربيعية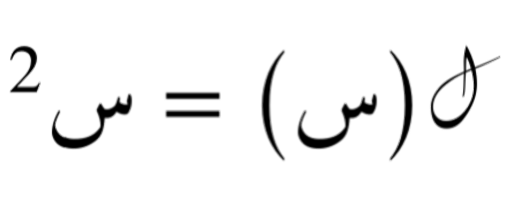
الآن، إذا قمنا بتركيب الدالتين، نحصل على دالة جديدة تُعبر عن العلاقة بين المتغيرات بطريقة أكثر تعقيدًا. تركيب الدالتين يُعطينا: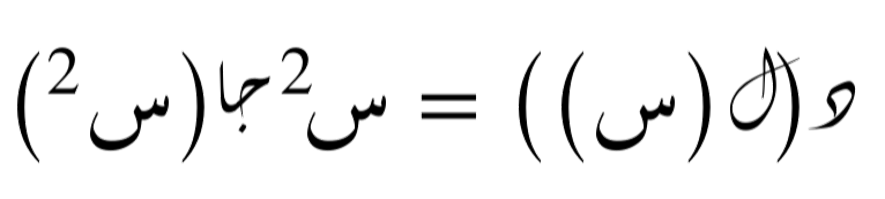
.
في هذا المثال، تركيب الدالتين يُظهر كيف يمكن أن تؤثر الدالة الجيبية على سلوك الدالة التربيعية. النتيجة هي دالة جديدة تجمع بين خصائص الدالتين الأصليتين.
مثال آخر
في هذا المثال نركّب ثلاث دوالّ:
مع التذكير بأن معكوس الدالة الثانية هو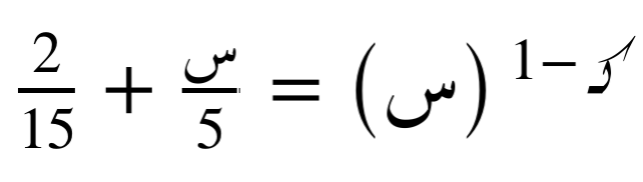
، وهو يمثل سعة الدالة الجيبية الأولى، حيث يؤدي إلى إلغائها، فتصبح لدينا سعة تتغير خطيًا عند تركيب الدوال.
