أنواع خاصة من الدوّال
الدوال المُعَلَّمَة
الدوال المُعلَّمة هي دوال رياضية تعتمد على متغيرات مستقلة بالإضافة إلى متغيرات أخرى تُعرف بالمعلمات، وتُستخدم هذه المعلمات لضبط خصائص الدالة أو سلوكها دون أن تُعدّ متغيرات حرة. تُستخدم الدوال المُعلَّمة على نطاق واسع في النمذجة الرياضية، والإحصاء، والتعلم الآلي، حيث تُمثّل المعلمات خصائص قابلة للتعديل لتحقيق أهداف معينة.
نعبّر عن دالّة معلّمة بالشكل التالي: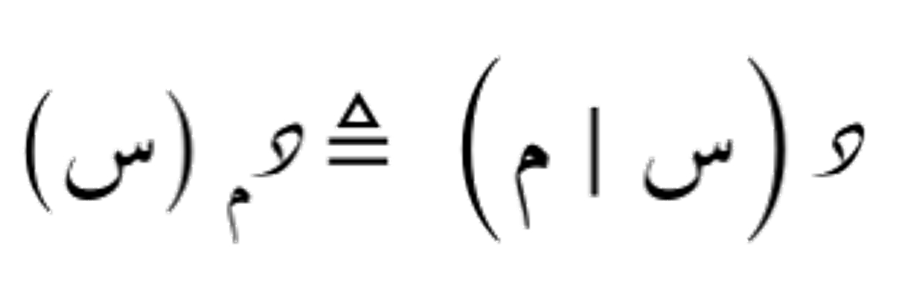
حيث م هو المعلّم أو المعامل.
مثال على الدوال المُعلَّمة
على سبيل المثال، يمكننا دراسة الدالة التالية:
والتي إذا أضفنا إليها معاملًا م، تصبح بالشكل التالي ونعرضها في الرسم على شكل عدّة منحنيات حسب تغيّر قيمة المعامل.
نعرضها أيضا على شكل رسم متحرّك يظهر لنا تغيّر سلوك الدالة مع تغيّر م.
مثال لآخر
الدالة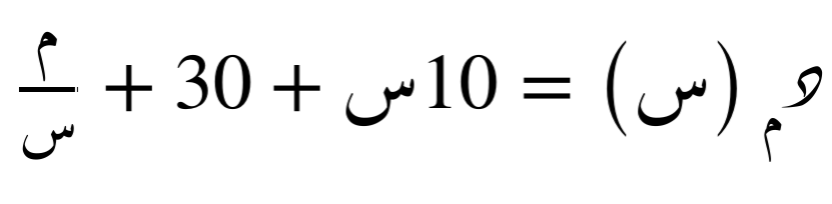
هي دالة مُعلَّمة حيث:
الدوال الحدودية
الدوال الحدودية هي نوع من الدوال الرياضية التي تُعبّر عن علاقة بين متغيرات باستخدام حدود متعددة. تُستخدم هذه الدوال في العديد من المجالات، بما في ذلك الرياضيات، والفيزياء، والهندسة، والاقتصاد. تتميز الدوال الحدودية بأنها تتضمن معاملات ثابتة ومتغيرات، ويمكن أن تكون خطية أو غير خطية حسب درجة الحدود.
يحدد الحد ذو الدرجة الأعلى في الدالة الحدودية شكل المنحنى عند القيم الكبيرة للمتغير، حيث يسيطر هذا الحد على سلوك الدالة كلما ابتعدنا عن نقطة الأصل.
الدوال الأسية
نتأمل هنا في تأثير تغيير المعامل م على الدالة الأسية إذا ما كان المعامل المتغيّر هو الأُس أو القُوّة المرفوع إليها العدد:
أو إذا كان الأس سالبا
الدوالّ الأسية واللوغارتمية
الدوالّ الدورية المثلثية
الدوال الدورية المثلثية هي دوال تتكرر قيمها على فترات منتظمة وتُستخدم لوصف الظواهر الدورية مثل الحركة الموجية والصوت والضوء. من أشهر هذه الدوال: الجيب (جا)، وجيب التمام (جتا)، والظل (ظا).
- الدورة: هي المدة أو المسافة التي تستغرقها الدالة لإكمال دورة كاملة قبل أن تبدأ في التكرار.
- النبضة: تشير إلى تغير سريع ومؤقت في قيمة الدالة، وغالبًا ما تُستخدم في الإشارات المربعة أو الموجات النبضية.
- التردد: هو عدد الدورات التي تحدث في وحدة الزمن، ويُقاس عادةً بالهرتز.
- السِعة: هي القيمة العظمى التي تصل إليها الدالة من نقطة التوازن (المحور الأفقي).
- الطور: هو الإزاحة الأفقية للدالة بالنسبة إلى نقطة الأصل، ويحدد مكان بدء الدورة.
مثال على الدوال المثلثية
الدالة المثلثية الجيبية تُعبر عن العلاقة بين الزاوية وطول الضلع المقابل في مثلث قائم الزاوية. يمكننا تمثيلها رياضيًا بالشكل التالي:
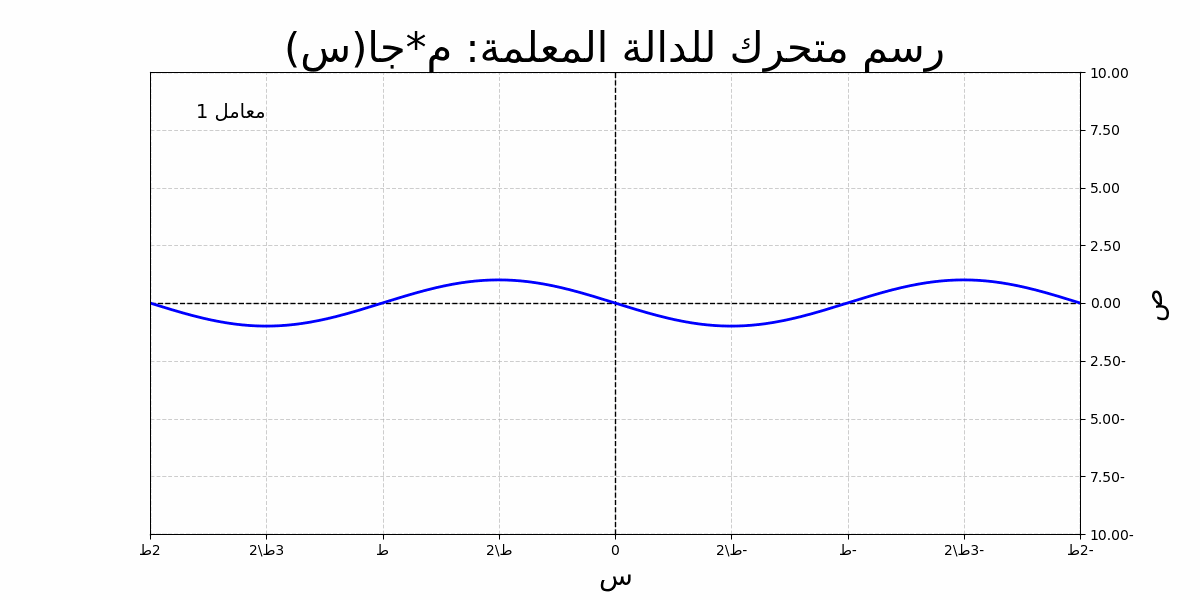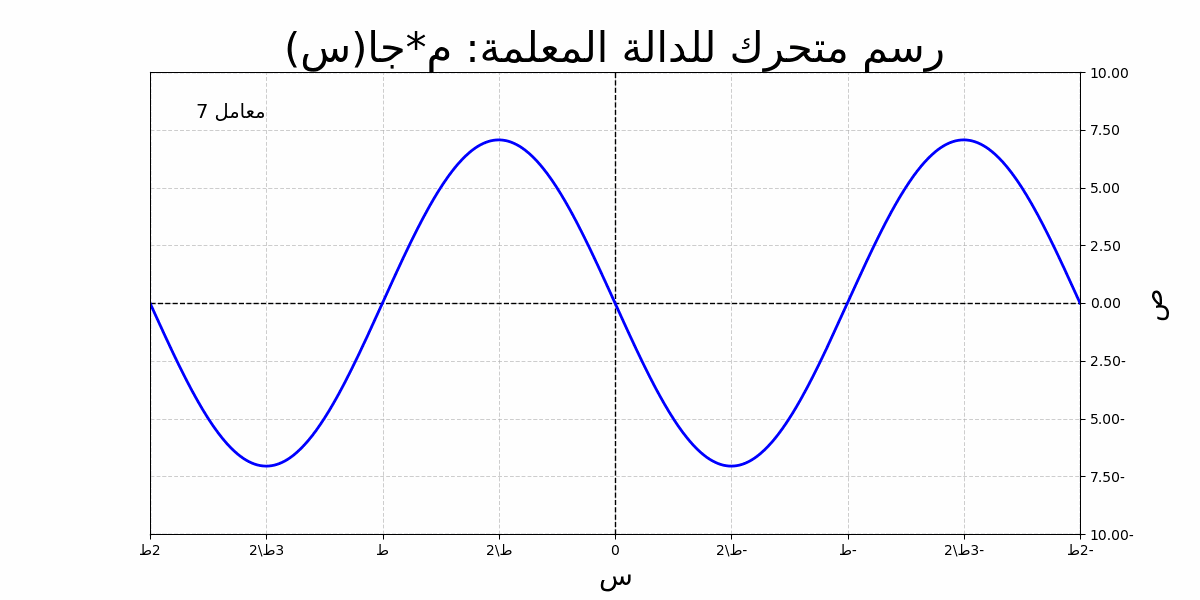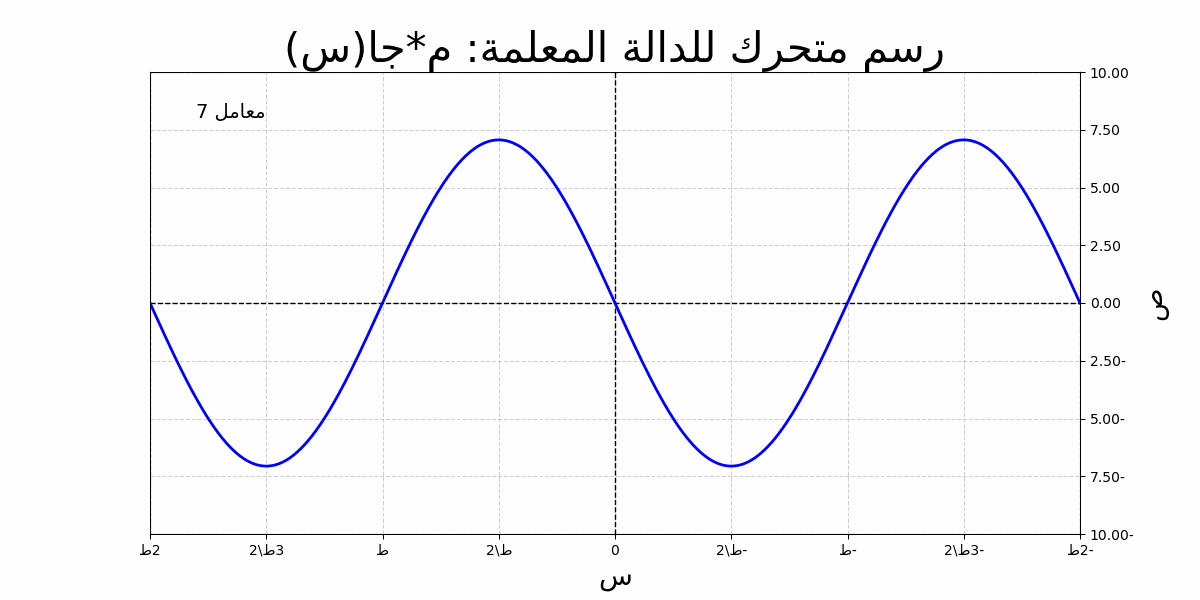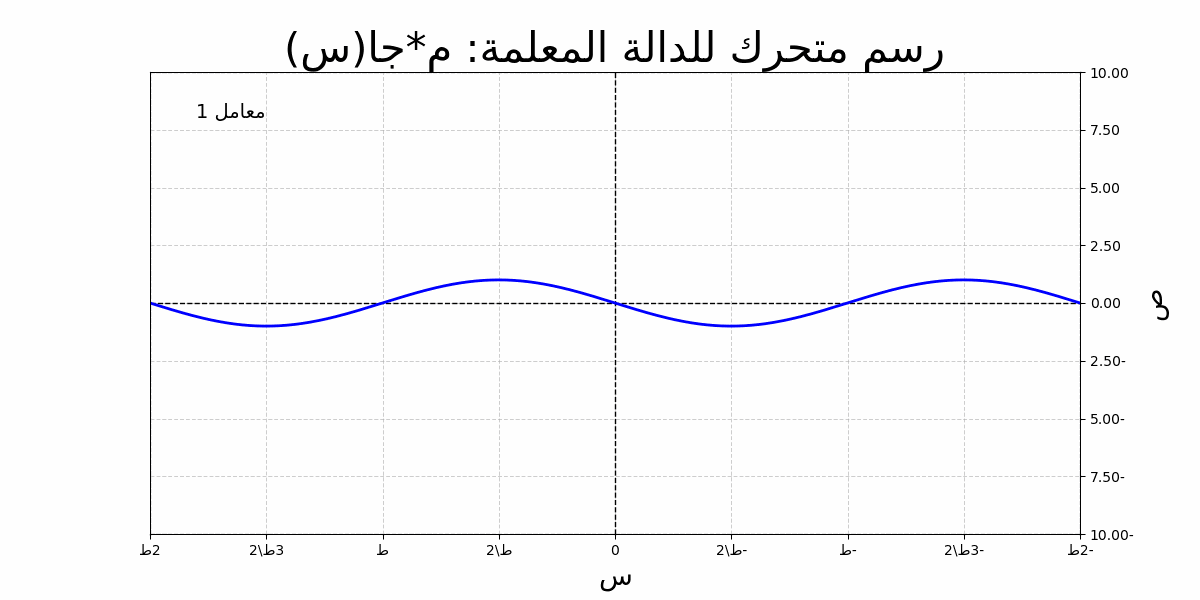
دالة الجيب مع توضيح السعة