الدوّال
الدوال
الدالة هي قاعدة رياضية تربط كل عنصر من مجموعة المُدخلات (مجال التعريف) بعنصر واحد فقط في مجموعة المُخرجات (المدى أو المجال المقابلة). يُرمز إلى الدالة بالشكل:
مجالات الدوال
- مجال تعريف الدالة
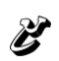هو مجموعة المُدخلات التي يمكن للدالة قبولها. بمعنى آخر، هو مجموعة القيم التي يمكن أن تُدخل في الدالة. - المجال المقابل للدالة
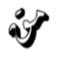هو مجموعة المخرجات التي يمكن أن تنتجها الدالة. بمعنى آخر، هو مجموعة القيم التي يمكن أن تعطيها الدالة عند تطبيقها على عناصر من مجالها. مدى الدالة هو جميع القيم الفعلية التي تأخذها الدالة (قد يكون مجموعة جزئية من المجال المقابل)
مثال
لنفترض أن لدينا الدالة التالية:
في هذه الحالة:
- مجال تعريف الدالة هو جميع الأعداد الحقيقية (مع)، لأننا يمكننا إدخال أي عدد حقيقي في الدالة.
- المجال المقابل للدالة هو جميع الأعداد الحقيقية (مق)، لأن الدالة يمكن أن تعطي أي عدد حقيقي كخرج.
- مدى الدالة هو جميع الأعداد الحقيقية الموجبة، لأن الدالة ترفع أي عدد حقيقي إلى القوة الثانية.
تصنيف الدوال حسب العلاقة بين المجموعات
- دالة متباينة (واحدية): هي الدالة التي تربط كل عنصر من مجال التعريف بعنصر مختلف في المجال المقابل، أي لا يوجد عنصران مختلفان في المجال لهما نفس الصورة في المجال المقابل.
- دالة شاملة: هي الدالة التي يكون لكل عنصر في المجال المقابل على الأقل عنصر واحد في مجال التعريف يرتبط به، أي أن صورة الدالة تغطي كامل المجال المقابل.
- دالة تقابلية: هي الدالة التي تحقق خاصيتي التباين والشمول معًا، أي أن كل عنصر في المجال المقابل يرتبط بعنصر واحد فقط في مجال التعريف، وبالتالي تكون الدالة قابلة للعكس (لها دالة عكسية).
الدوال العكسية
الدالة العكسية هي دالة تعكس تأثير الدالة الأصلية. إذا كانت الدالة الأصلية تأخذ قيمة معينة وتنتج قيمة أخرى، فإن الدالة العكسية تأخذ هذه القيمة الناتجة وتعيدها إلى القيمة الأصلية.
يكون للدالة دالة عكسية إذا وفقط إذا كانت تقابلية. بحيث تحقق:
لنفترض أن لدينا الدالة التالية:
وهي دالة تقابلية حيث:
الدالة العكسية لها الشكل:
التزايد والتناقص
التزايد
الدالة تكون متزايدة إذا كانت قيمها تزداد كلما زادت قيم المدخلات. بمعنى آخر، إذا كانت س١ < س٢ تؤدي إلى د(س١) < د(س٢).
- دالة متزايدة:إذا كان لكل قيمتين س١ < س٢ يكون د(س١) ≤ د(س٢).
- دالة متزايدة تماماً:إذا كان لكل قيمتين س١ < س٢ يكون د(س١) < د(س٢).
لنفترض أن لدينا الدالة التالية:
في هذه الحالة:
- الدالة متزايدة تماماً على المجال (
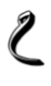) كلّه لأن كلما زادت قيمة س، تنخفض قيمة د(س).
التناقص
الدالة تكون متناقصة إذا كانت قيمها تنخفض كلما زادت قيم المدخلات. بمعنى آخر، إذا كانت س١ < س٢ تؤدي إلى د(س١) > د(س٢).
- دالة متناقصة:إذا كان لكل قيمتين س١ < س٢ يكون د(س١) ≥ د(س٢).
- دالة متناقصة تماماً:إذا كان لكل قيمتين س١ < س٢ يكون د(س١) > د(س٢).
لنفترض أن لدينا الدالة التالية:
في هذه الحالة:
- الدالة متناقصة تماماً على المجال (0, ∞) أو (
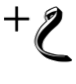) فقط لأن كلما زادت قيمة س، تنخفض قيمة د(س).
النهايات
النهاية هي مفهوم رياضي يصف سلوك الدالة عندما تقترب المدخلات من قيمة معينة. يمكن أن تكون النهاية موجودة أو غير موجودة: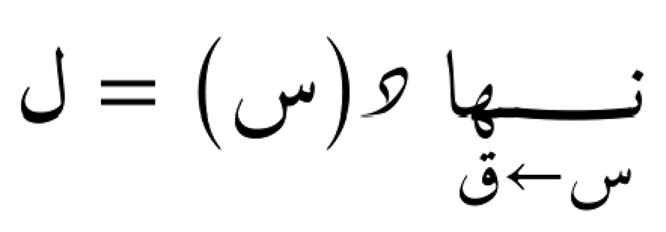
أي أن القيم التي تأخذها الدالة تقترب من العدد ل عندما يقترب س من ق.
أنواع النهايات:
- نهايات محدودة: تصل إلى قيمة عددية معينة.
- نهايات غير محدودة: تذهب إلى اللانهاية أو السالب لانهاية.
- نهايات من جهة واحدة: النهاية عند الاقتراب من اليمين أو من اليسار فقط.
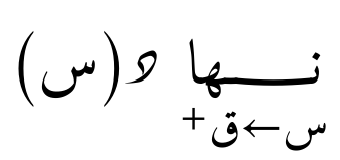أو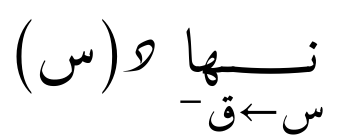
الإستمرارية
الدالة تكون مستمرة إذا كانت قيمها لا تتغير بشكل مفاجئ. بمعنى آخر، إذا كانت النهاية للدالة عند نقطة معينة تساوي قيمة الدالة عند تلك النقطة من الجهتين معاً: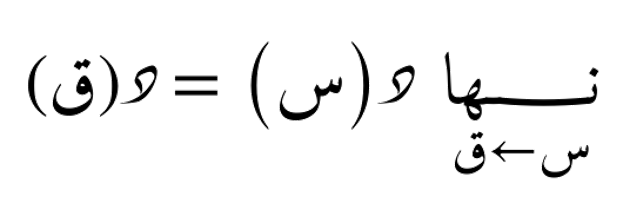
المثال ألأوّل
الدالة التالية مستمرة عند النقطة س=0، لأن الدالة نفسها مُعرّفة بصغتين مختلفتين عن يمين وعن يسار الصفر.
المثال الثاني
الدالة التالية غير مستمرة عند النقطة س=2، لأن النهاية من اليمين لا تساوي النهاية من اليسار.
السلوك المقارب
السلوك المقارب هو مفهوم رياضي يصف كيف تقترب الدالة من قيمة معينة عندما تقترب المدخلات من نقطة معينة. يمكن أن يكون السلوك المقارب إما من الأعلى أو من الأسفل.
يوجد نوعان رئيسيان من السلوك المقارب: مقارب أفقي عندما تقترب الدالة من قيمة ثابتة مع زيادة أو نقصان المتغير، ومقارب رأسي عندما تقترب قيم الدالة من اللانهاية عند اقتراب المتغير من قيمة معينة.
المثال الأول
الدالة التالية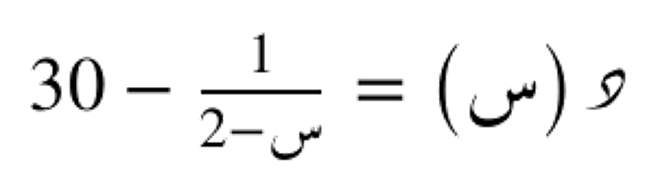
لها مقارب أفقي عند س=-30، ومقارب رأسي عند ص=2.
ذلك لأنّ
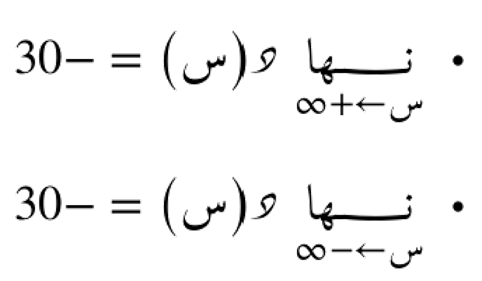و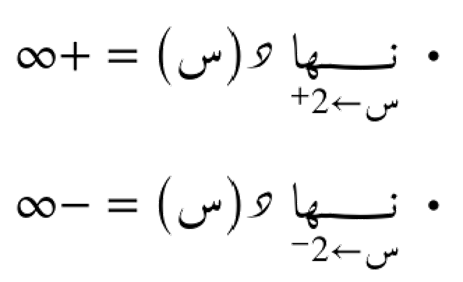
المثال الثاني
الدالة التالية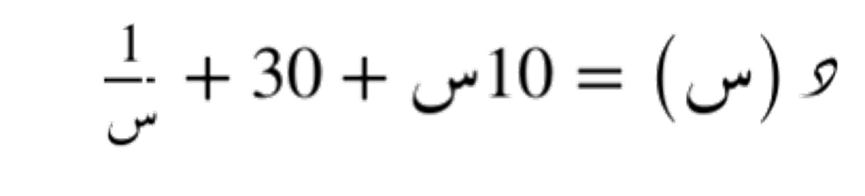
لديها مُقارب مائل و معادلته هي
