الدوالّ والحقول المُتجهية
في الأمثلة السابقة، تناولنا دوالّ تأخذ متجهًا مكوّنًا من عددين أو أكثر وتُعطي عددًا واحدًا كمخرج. في هذه الفقرة، سنستعرض دوالّ تأخذ متجهًا كمدخل وتُعطي أيضًا متجهًا كمخرج.
دوال المتجهية
الدوالّ المُتجهية هي دوال يكون مخرجها متجهًا، أي أن فضاء القيم الناتجة لها ذو بعد أكبر من واحد، بينما يكون مدخلها غالبًا عددًا واحدًا فقط (مثل متغيّر الزمن في الفيزياء). على سبيل المثال، يمكن أن تصف دالة متجهية موضع جسم متحرك في الفضاء بدلالة الزمن، بحيث تعطي لكل قيمة للزمن متجهًا يحدد موقع الجسم في تلك اللحظة.
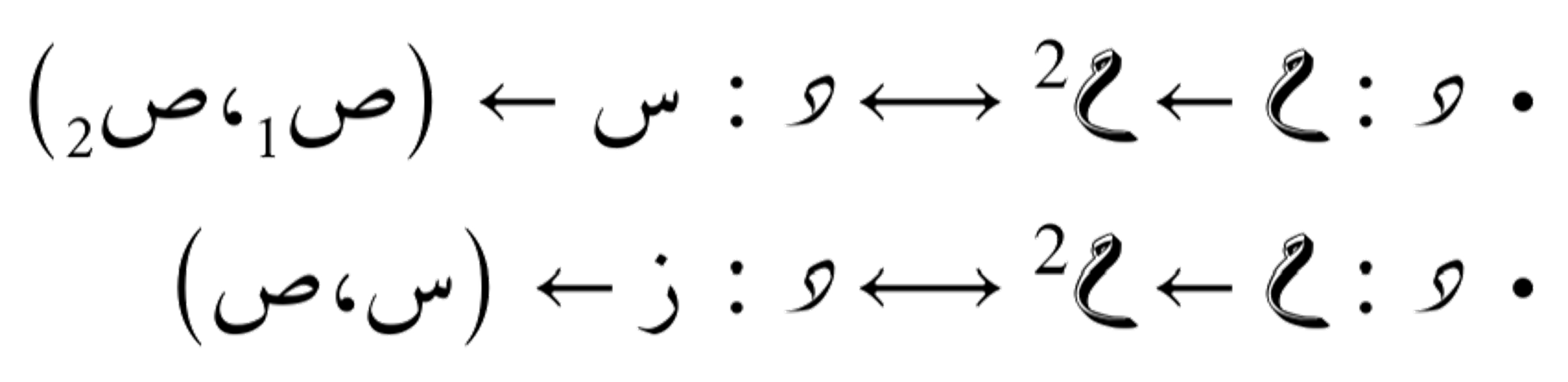
المسار الدائري الدوري
نعلم حتما، من مدارستنا للسطح العُقدي و دوران المتجهات على السطح، أنّ الدالتين الجيب والجيب التمام ترسمان مسار دائري. نتتبع مسار الإحداثيتين السينية والصادية معاً من خلال الدالة المتجهية التالية
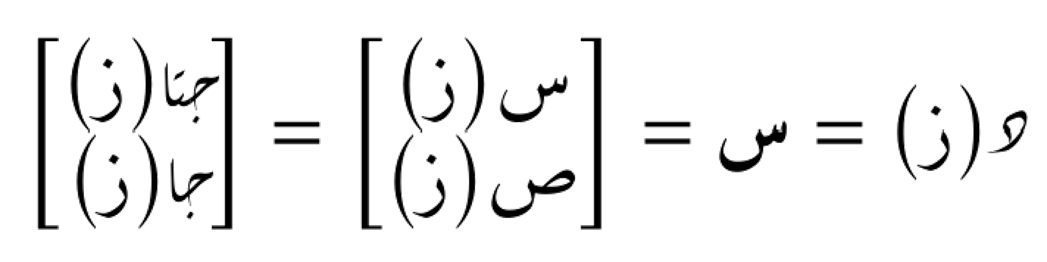
وعند تمثيل منحنيات هذه الدالة المتجهية على المستوى الإحداثي المتعامد، تظهر بهذا الشكل:
المسار الكُروي الحلزوني
ننتقل الآن إلى تمثيل نفس المسار في الفضاء ثلاثي الأبعاد، حيث نعرّف ثلاث دوالّ تصف الإحداثيات السينية والصادية والارتفاعية لمسار حلزوني كما هو موضّح في الشكل أسفله.
نلاحظ على المحاور الثلاثة كيف تتغير الإحداثيات بشكل متذبذب، حيث تتبع كل نقطة مسارها بدقة وفق الدوالّ التالية، مما ينتج منحنى حلزونياً متناسقاً في الفضاء الثلاثي الأبعاد.
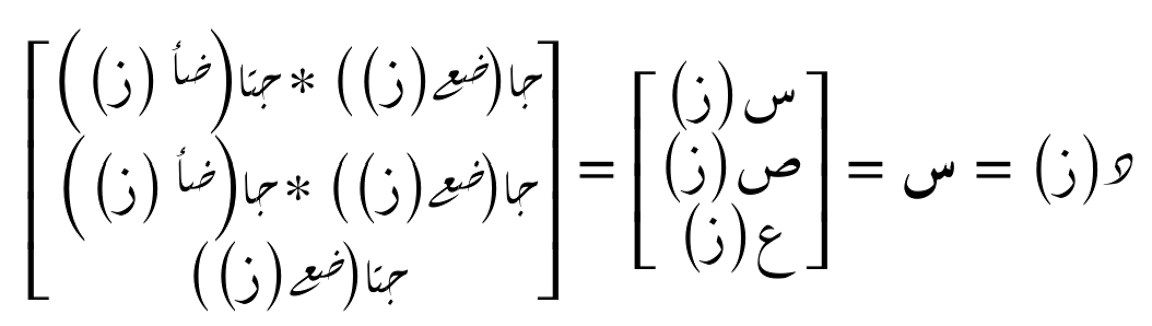
تُسمّى هذه الدوال دوالّ دورية لأنها تعتمد على متغير الزمن بشكل دوري، ويُحدّد تكرار هذا الدوران ما يُعرف بالنبضة (أو التردد الزاوي). العلاقة بين النبضة ض والتردد ف هي:
نُعرّف في هذا السياق نوعين من النبضات:
- النبضة الأفقية (ضأ): تتحكم في سرعة دوران الإحداثيتين السينية والصادية حول المركز.
- النبضة العمودية (ضع): تتحكم في سرعة تغير الإحداثي العمودي (الارتفاع)، وغالباً ما تكون أبطأ كما يظهر في الرسم التالي.
الحقول المُتجهية
الحقول المتجهية هي دوال تُنتج أيضا متجهات (فضاء مخرجات ذات بعد أكثر من واحد)، لكن من خلال مدخلات أيضا متعددة (أي متجهات غالبا ما تعبّر عن مكان في الفضاء، خاصة في مجال الفيزياء). على سبيل المثال، يمكن أن يكون لدينا حقل مُتجه يُعبر عن سرعة أو اتجاه الرياح في نقطة معينة في الفضاء، حيث يُعطى كل نقطة في الفضاء متجه سرعة.
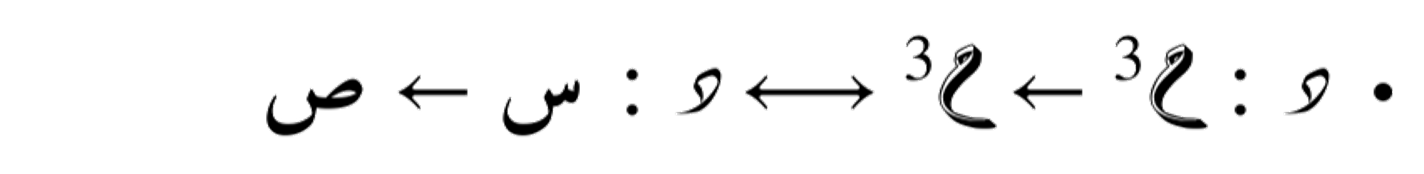
عرض مثل هذه الدوال يكون حرفيا برسم المتجه الناتج عن الدالة في مكان ما حيث أنّ طول وإتجاه المتجه في الفضاء يعبّران معا على سلوك الدالّة في النقطة المعيَّنة. تسمى هذه الرسوم حقول متجهات حيث نأخد عيّنات من الفضاء لنرسم متّجهاتها الناتجة عن الدالة.
على سبيل المثال الدالّة الثنائية الأبعاد التالية:
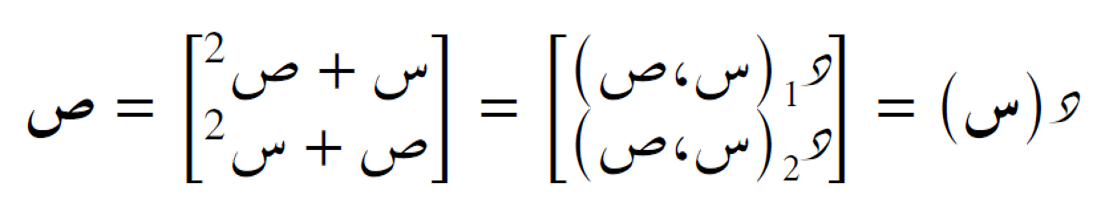
عند تمثيل هذا الحقل المتجه على المستوى الإحداثي، نحصل على رسم يُظهر اتجاه وقوة المتجهات في كل نقطة كما في الشكل:
في بعض الحالات، تتداخل المتجهات في الرسم بحيث يصعب تمييز اتجاهاتها أو أطوالها، فنلجأ أحيانًا إلى توحيد أطوال المتجهات (تطبيعها)، لكن بذلك نفقد معلومة السعة (الطول) الأصلية للمتجه.
لتعويض فقدان معلومة السعة، يمكننا تلوين المتجهات حسب مقياس لوني يعكس طول كل متجه، فيصبح المظهر أكثر تعبيرًا عن شدة المتجهات في كل نقطة.
نتمكن إذن من إقتناء عيّنات أكثر من الفضاء ليكون الرسم إذن أكثر تعبيرا عن الحقل المتجهي المدروس.
حقل متجهي ثلاثي الأبعاد
يمكن تمثيل الحقول المتجهية لدوال ثلاثية الأبعاد، وهو أمر شائع في مجالات العلوم الفيزيائية والهندسة. على سبيل المثال، يمكننا دراسة الحقل المتجه التالي:
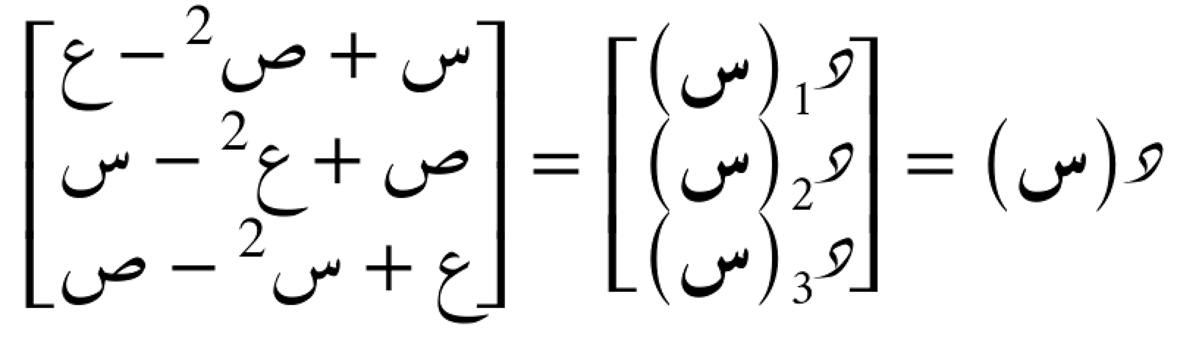
أما عندما تكون دوال الحقل المتجه ذات فضاء مخرجات بأبعاد أكبر من ثلاثة، يصبح من غير الممكن تمثيلها بصريًا بالشكل المباشر نفسه. في هذه الحالة، نلجأ عادة إلى إسقاط الأبعاد العالية على فضاء ثلاثي الأبعاد، ومن ثم نقوم بتمثيلها ورسمها بطريقة مناسبة لفهمها.
حقل متجهي زمني متحرك
يمكن كذلك النظر إلى الحقول المتجهية الزمنية المتحركة، والتي تنتشر بشكل واسع أيضا في تطبيقات الفيزياء والهندسة، خاصة عند دراسة الظواهر التي تتغير مع الزمن مثل انتشار الأمواج أو حركة الموائع. تكون الدوال المتحكمة في مثل هذه الحقول بدلالة متغيّرات الزمان والمكان. كمثال على ذلك، يمكننا تمثيل الحقل المتجهي الزمني المتغيّر التالي:










