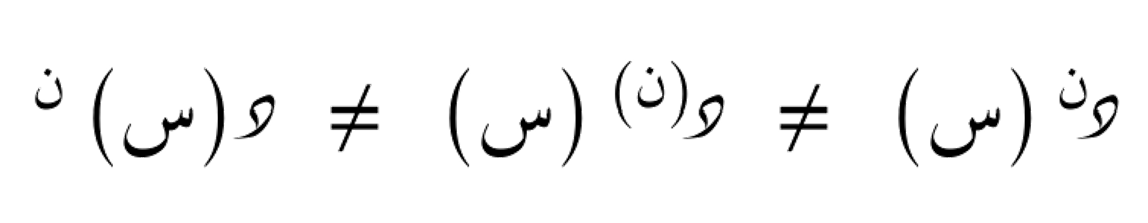المتسلسلات
المتسلسلات هي مجموعات من الحدود التي تتبع نمطًا معينًا. يمكن أن تكون هذه الحدود أعدادًا حقيقية أو مركبة، وتُستخدم في العديد من التطبيقات الرياضية والفيزيائية.
أنواع المتسلسلات
متسلسلة الجمع
تعتمد على جمع دوال متعددة أو متكررة ضمن سلسلة واحدة، وتُستخدم بشكل رئيسي في التقريبات الرياضية، مثل المتسلسلة الحدودية التفاضلية و المتسلسلة الطيفية التوافقية والتي تشمل إشتقاقات وتكاملات، مفاهيم يتم شرحها وعرضها في الفقرات القادمة إن شاء الله.
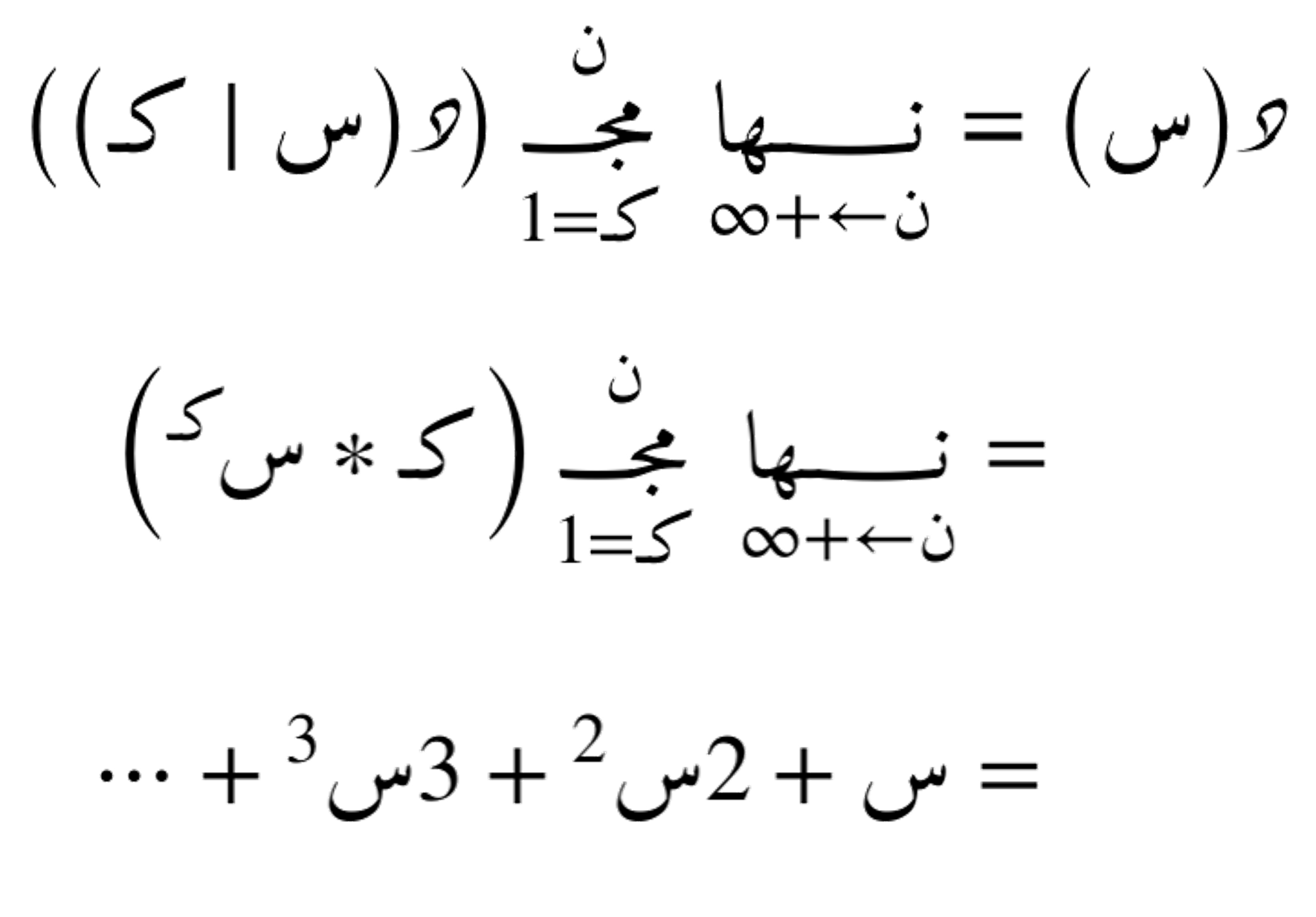
المتسلسلة الحدودية التفاضلية:
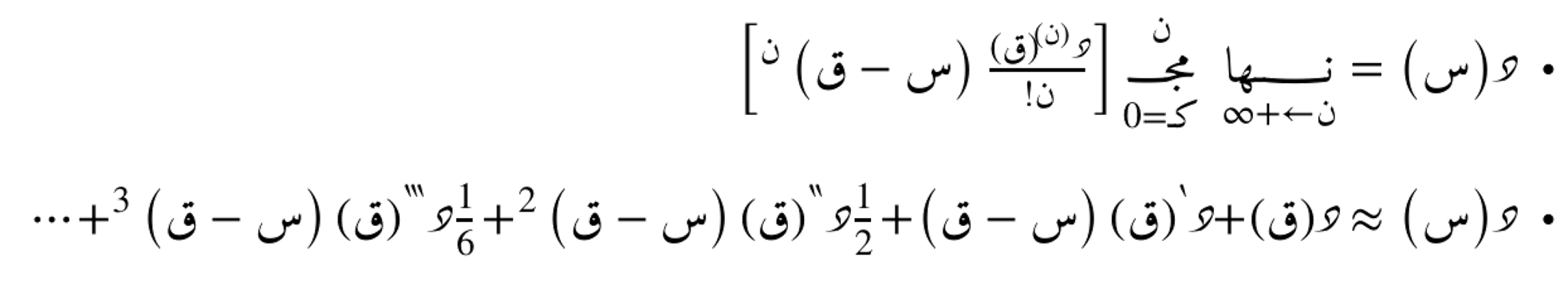
المتسلسلة الطيفية التوافقية:
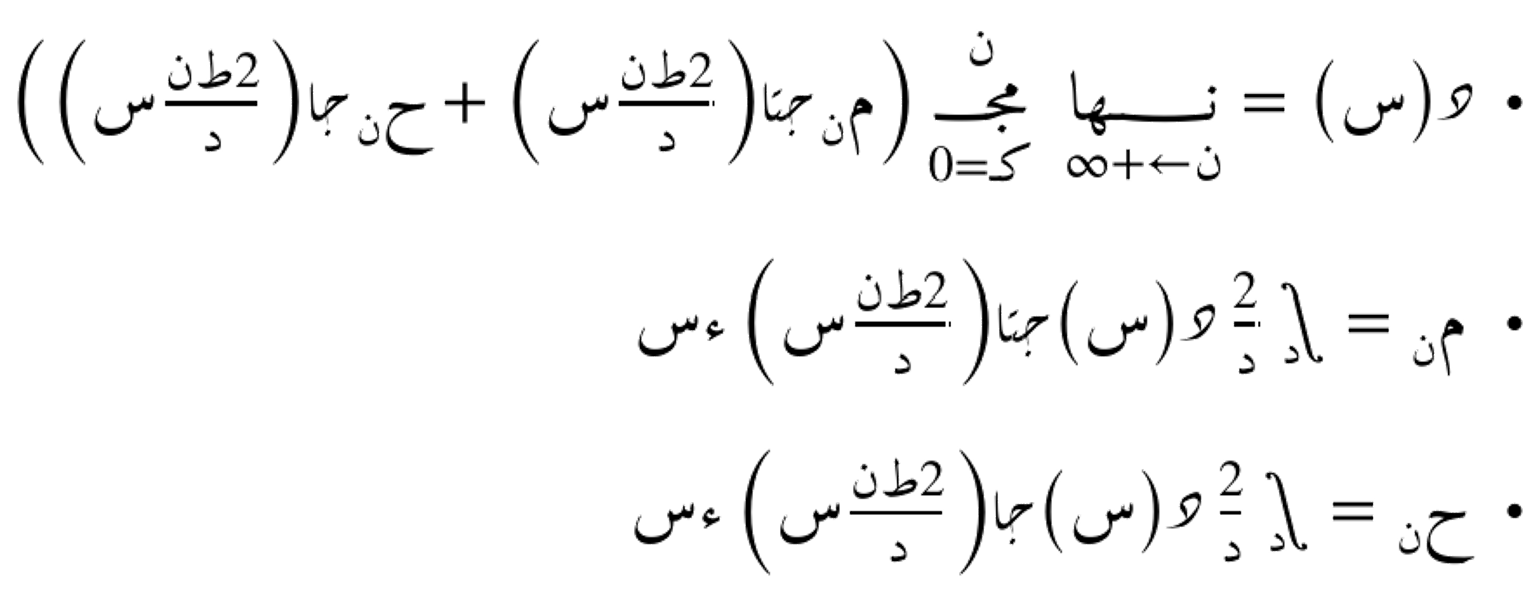
مع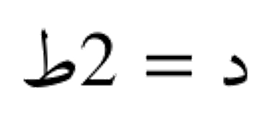
متسلسلات الضرب
تُبنى على أساس ضرب الدوال مع بعضها بشكل متسلسل، وتظهر غالباً في التحليل الرياضي ونظرية الأعداد. يُستخدم هذا النوع لتمثيل دوال خاصة أو التعبير عن خصائص رياضية عميقة، مثل الصيغ اللانهائية.
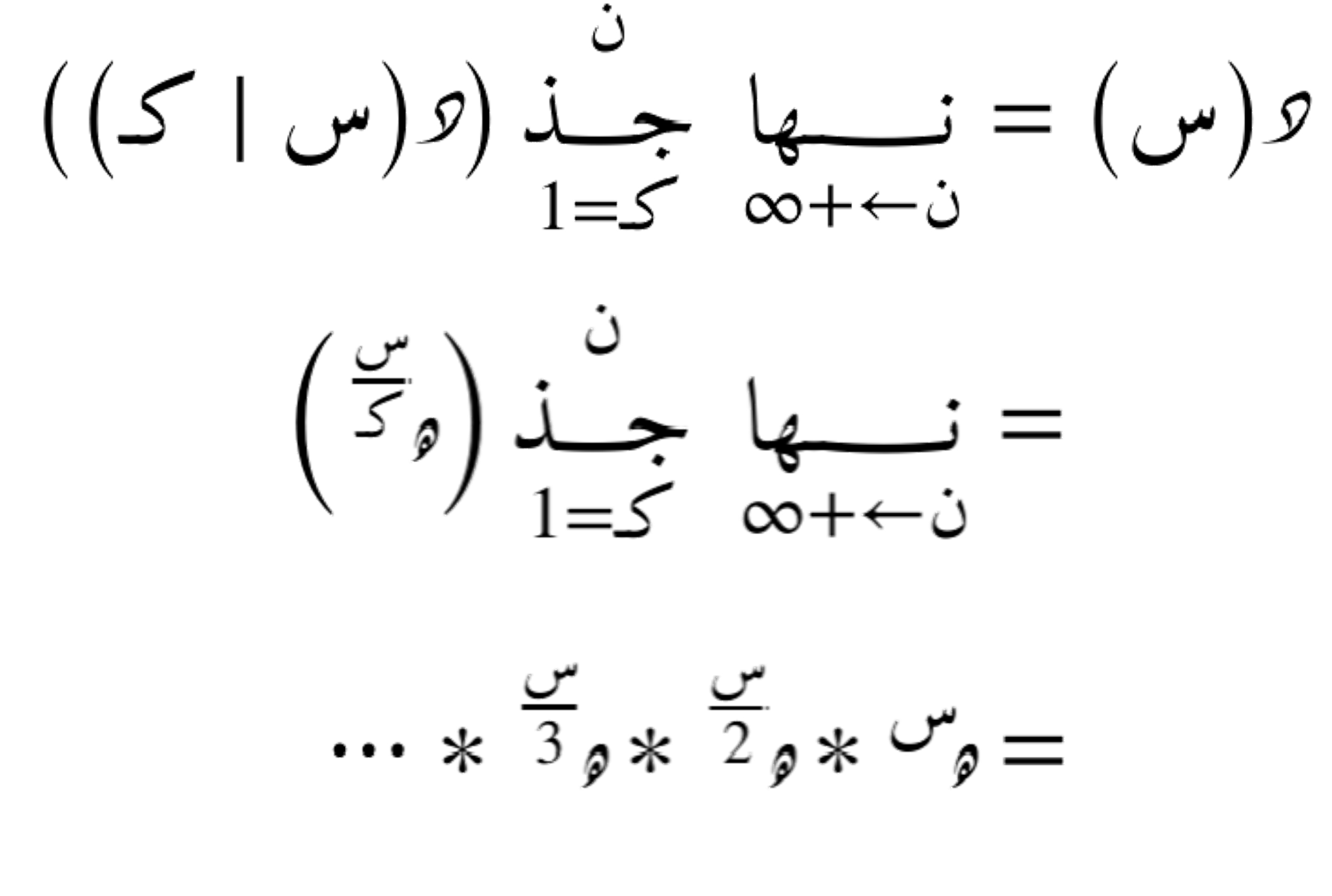
متسلسلات التضمين (التراكب التكراري)
تقوم على تكرار تركيب دالة داخل أخرى عدة مرات، بحيث تصبح كل دالة جزءاً من دالة أكبر ضمن تسلسل تراكبي، ويظهر هذا النوع في الأنظمة الديناميكية ودراسة الاستقرار والتقارب، بالإضافة إلى تحليل السلوك طويل الأمد للنظم الرياضية.
يُرجى عدم الخلط بين الرموز المستخدمة: فترميز تراكب الدوال (التضمين) يختلف عن ترميز مشتقات الدوال وكذلك عن ترميز رفع الدالة إلى قوة، كما هو موضح في الصورة أدناه من اليمين إلى اليسار.
