طرق بناء الأسطح من منحنيات ثلاثية الأبعاد
الأسطح الناعمة
مقدّمة
السطح الناعم يُفهم ككائن ثنائي الأبعاد مغمور في فضاء ثلاثي الأبعاد، ويُوصف بواسطة دوال قابلة للاشتقاق بشكل كافٍ. التمثيل البارامتري العام يكون:
د(ز, غ) = (س(ز, غ), ص(ز, غ), ع(ز, غ))
حيث ز وغ متغيران معلِّمان يُغطيان بُعدَي السطح.
مضامين
في هذه الصفحة نستعرض طرق بناء الأسطح من منحنيات ثلاثية الأبعاد. الطُرُق المعروضة هُنا تشمل:
- السحب المساري
- • البثق الخطي
- • السحب العام
- التلبيس
- • التلبيس الخطي
- • التلبيس المبني على ثنائيات الحدّين
- • التلبيس المبني على العقد
- الأسطُح المبنية مباشرة من نقاط
- • الأسطح المبنية على ثنائيات الحدّين
- • الأسطح المبنية على العقد
كل طريقة لها استخداماتها الخاصة حسب نوع البيانات المتاحة، سواء كانت منحنيات معرفة بدقة أو مجموعة نقاط مأخوذة من بيانات تجريبية.
السحب المساري
البثق الخطي
بثق المنحنى هو عملية مد منحنى ثنائي الأبعاد على طول خط مستقيم لإنشاء سطح ثلاثي الأبعاد. مثال: بثق دائرة على طول المحور ع ينتج أسطوانة.
معادلة البثق الخطي هي:
حيث د(ز) دالة تمثل موقع النقطة على المنحنى في بعد ز و م المتجه الذي يُوجّه البثق ويُحدد إتجاهه.
أسفله مثال على بثق منحنى في إتجاهات مختلفة:
السحب العام
السحب العام هو تعميم لعملية البثق حيث يُنقل منحنى المقطع على طول مسار منحني في الفضاء ثلاثي الأبعاد مع السماح بتحولات مثل التدوير والتدرج في الحجم.
لتكن الدالة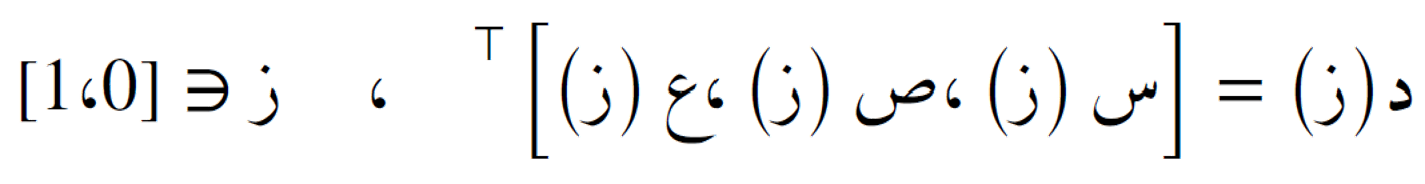
دالة المنحنى المسحوب.
و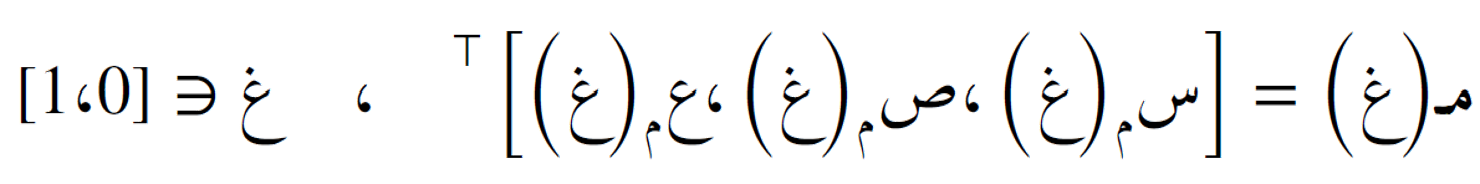
دالة المسار المتتبَّع.
معادلة السحب العام إذن هي:
حيث مـد(غ) هي مصفوفة الدوران التي تحدد توجه القطعة المسحوبة إزاء سحبها على طول المسار المتتبع. فتكون في أبسط الحالات هي المصفوفة الوحدة أي أن المنحنى المسحوب يحتفظ بنفس التوجه على طول المسار.
و مـل(غ(ي)) هي مصفوفة الإلتفاف التي تحدد كيفية التفاف القطعة المسحوبة حول المسار المتتبع.
و ح(غ) هي دالة التحجيم التي تحدد كيفية تغيير حجم القطعة المسحوبة على طول المسار المتتبع.
ملاحظة
عند إنعدام الدوران أو تغيير لحجم القاعدة عبر المسار وإذا ما كان المسار نفسه عبارة عن خط مستقيم، فإن السحب العام يصبح بثقاً خطياً.
مثال لمصفوفة الدوران
مثال لمصفوفة الإلتفاف
مثال لدالة التحجيم
مثال: سحب دائرة على طول مسار حلزوني
التلبيس
التلبيس الخطي
يتم إنشاء سطح بربط منحنيين أو أكثر بخطوط مستقيمة أو تدرجية، حيث يمثل كل مقطع عرضي منحنى معين وهو تلبيس مبني على ثنائيات الحدّين من الدرجة الأولى.
منحنى التلبيس بين منحنيين في اتجاه ز
منحنى التلبيس بين منحنيين في اتجاه غ
التلبيس المبني على ثنائيات الحدّين
الدرجة ثانية: تلبيس تربيعي بين ثلاث منحنيات
يتم استخدام ثنائيات الحدّين للحصول على العبارة: لتوليد سطح ثلاثي الأبعاد يمر عبر ثلاث منحنيات.
الدرجة النونية
مع
التلبيس المبني على العقد
يعتمد على تحديد مجموعة "عُقد" في الفضاء وتوليد سطح يمر بها أو يتأثر بها بطريقة مرنة.
الأسطح المبنية مباشرة من نقاط
الأسطح المبنية على ثنائيات الحدّين
يُولَّد سطح بيزييه من شبكة مستوية من النقاط (عُقد تحكم)، حيث يُحسب كل موضع على السطح كمزيج وزني لهذه النقاط باستخدام دوال بيرنشتاين في الاتجاهين. كل نقطة على السطح تُعطى بالصيغة:
حيث
نقاط التحكم، و
و
هي دوال بيرنشتاين في الاتجاهين ز و غ. كلما زاد عدد النقاط، أصبح السطح أكثر مرونة وتعقيدًا.
الأسطح المبنية على العقد
تُستخدم مجموعة من النقاط (العقد) لتحديد سطح ثلاثي الأبعاد، حيث يتم استخدام دوال أساس مثل المبنية على العقد مع أوزان لتحديد شكل السطح. هذه الطريقة تسمح بمرونة أكبر في تصميم الأسطح لتوليد السطح.
حيثنقاط التحكم، و
و
هي دوال مبنية على العقد في الاتجاهين ز و غ، مع درجات م1 و م2 على التوالي. كلما زاد عدد النقاط أو درجة الدوال، أصبح السطح أكثر مرونة وتعقيدًا.
جدول ملخص
| الطريقة | الوصف | المعادلة |
|---|---|---|
| السحب المساري - البثق الخطي | استيفاء خطي بين منحنيات متعاقبة | |
| السحب المساري - السحب العام | استيفاء منحنيات بشكل عام عبر مسار | |
| التلبيس - التلبيس الخطي | سطح مبني من وصلات خطية بين المنحنيات | |
| التلبيس - ثنائيات الحدّين | سطح باستعمال ثنائيات الحدّين | |
| التلبيس - المبني على العقد | استعمال العقد لتحديد شكل السطح | |
| الأسطح المبنية من نقاط - ثنائيات الحدّين | سطح مبني من نقاط باستخدام ثنائيات الحدّين | |
| الأسطح المبنية من نقاط - العقد | سطح مبني من نقاط باستخدام العقد |
