القِيَم الذاتية

في هذا الدرس، سوف نتناول مفهوم القيم الذاتية والمصفوفات الذاتية. هذه المفاهيم تلعب دورًا مهمًا في العديد من التطبيقات في الرياضيات والفيزياء والهندسة.

يعرض الفيديو أعلاه تمثيلاً بصرياً لتحويل خطي في بعدين، حيث تظهر متجهات القيم الذاتية للمصفوفة المحوِّلة باللون الأسود. عند تطبيق التحويل الخطي، تلاحظ أن هذين المتجهين لا يتغير اتجاههما، بل يتغير طولهما فقط، أي أنهما يتمددان أو ينكمشان دون أن يدورا. هذا السلوك يوضح الخاصية الأساسية للمتجهات الذاتية: فهي المتجهات التي لا يتغير اتجاهها تحت تأثير التحويل الخطي، بل تتغير أطوالها بمقدار يساوي القيمة الذاتية المرتبطة بكل متجه ذاتي. يُعد هذا التصور البصري أداة مهمة لفهم دور المتجهات والقيم الذاتية في دراسة التحويلات الخطية.

المتجه الذاتي لمصفوفة هو متجه لا يتغير اتجاهه عند تطبيق التحويل الخطي الذي تمثله تلك المصفوفة. بمعنى آخر، إذا كان مـس هي مصفوفة وس هو متجه ذاتي، فإن العلاقة التالية صحيحة:

حيث م هو القيمة الذاتية المرتبطة بالمتجه الذاتي س.

لإيجاد القيم الذاتية والمتجهات الذاتية لمصفوفة مربعة، نكتب معادلة القيم الذاتية العامة عبر طرح م مضروبة في مصفوفة الوحدة (مـو) من المصفوفة الأصلية، ثم نحسب محدد هذه المصفوفة الجديدة ونساويه بالصفر للحصول على معادلة القيم الذاتية (المعادلة المميزة)، وبعد حلها نجد القيم الذاتية، ثم نعوض بكل قيمة ذاتية في المعادلة الأصلية لإيجاد المتجهات الذاتية الموافقة كما سنرى في المثال الآتي.

✦مثال

دعنا نأخذ مثالاً عمليًا لتوضيح هذه الخطوات:

عادةً ما يكون عدد القيم الذاتية والمتجهات الذاتية لمصفوفة مربعة مساوياً لعدد أبعادها، لكن قد لا تكون جميع المتجهات الذاتية خطياً مستقلة. لنأخذ المثال التالي لمصفوفة مربعة، مع ملاحظة أننا لا نحسب القيم الذاتية إلا للمصفوفات المربعة: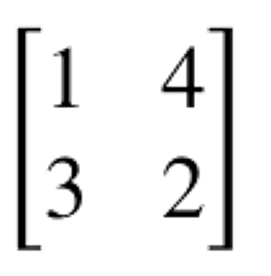

نبدأ بجبر القيمتين الذاتيتين من خلال حساب محدد المصفوفة التالية. م هنا هو قذ للإشارة إلى القيمة الذاتية.

ثم نعوّض بكل قيمة ذاتية في المعادلة الأصلية لإيجاد المتجهات الذاتية الموافقة كما سنرى في المثال الآتي بالنسبة للقيمة الذاتية 5 والتي تعني أن المتجه الذاتي الموافق لها يتمدد بخمس أضعاف عند تحويل المصفوفة للفضاء دون أن يتغيّر اتجاهه.

هكذا نجد أن المتجه الذاتي الموافق للقيمة الذاتية 5 هو: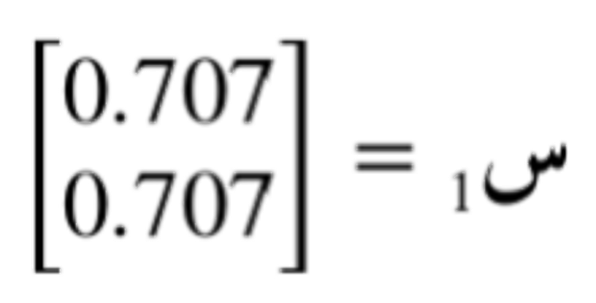

وبالمثل، يمكننا حساب المتجه الذاتي للقيمة الذاتية الأخرى 2 بنفس الطريقة. فنجد أن المتجه الذاتي الموافق لها هو: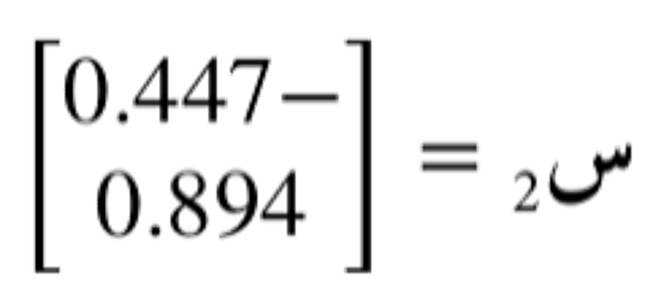

و هذان المتجهان هما المتجهات الذاتية للمصفوفة المعطاة، حيث يمثل كل منهما اتجاهًا لا يتغير تحت تأثير التحويل (أنظر الفيديو في أعلى الصفحة).

يمكن إعادة كتابة المعادلتين السابقتين في صيغة تحليل القيم الذاتية كما يلي:

حيث تمثل المصفوفة القطرية مقذ القيم الذاتية، والمصفوفة الأخرى ممذ أعمدتها هي المتجهات الذاتية.

يمكن إذن كتابة المصفوفة الأصلية على شكل مـس = ممذ مقذ ممذ^-1

وهذا يعني أن المصفوفة يمكن تحليلها إلى منتج من ثلاث مصفوفات: المصفوفة التي تحتوي على المتجهات الذاتية، المصفوفة القطرية التي تحتوي على القيم الذاتية، والمصفوفة المعكوسة للمتجهات الذاتية. هذا الذي يسمّى بتحليل أو تفريق القيَم الذاتية لمصفوفة.

✦ملحوظة

إذا كانت المصفوفة مـس مُتناظرة، فإن جميع القيم الذاتية لها حقيقية، ويمكن اختيار ترتيب المتجهات الذاتية في المصفوفة ممذ لتكون هذه الأخيرة متعامدة حيث.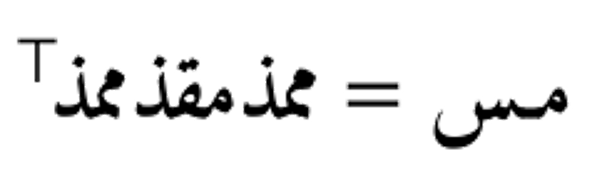

يمكن إذن العرض التحويلة الخطية للمصفوفة على شكل ثلاث تحويلات خطية متاتالية آخرها يطابق التحويلة الأصلية: تدوير ثم تمدد ثم تدوير ثان

نختار المصفوفة الثلاثية الأبعاد التالية:

و هي مصفوفة متعامدة أي أنّ، كما سبق الشرح، تحويلها الخطي للفضاء الثلاثي هو عبارة عن تدوير فقط بدون أي تمدد أو تقلّص.

نحسب قيمها الذاتية أوّلا وعددها ثلاثة لاكن بما أنّ المصفوفة غير متناظرة وكونها أيضا متعامدة، فإنّ سيكون بعض أو حتى كلّ قيَمها الذاتية مركّبة (عُقدية) ليس من الأعداد الحقيقية:

في هذه الحالة هناك قيمتان ذاتيتان لهذه المصفوفة هما عددين عقديين بينما الثالثة تساوي واحد لأنّ كما سبق الذكر أن المصفوفة المتعامدة تُبقي الفضاء في مقياسه بدون تمدد أو تقلّص فتُطبّق عليه عملية تدوير فقط. بعد حساب المتجهات الذاتية، نحصل أيضا على إثنان منهم عُقديان:

و المتجه الذاتي الثالث هو متجه حقيقي:

هذا المتجه إذا عرضناه في الفضاء الثلاثي الأبعاد سيمثل لنا محور الدوران. و إذا عرضنا المتجهات الذاتية الأخرى في الفضاء الثلاثي الأبعاد، فإنّها ستشكّل لنا مستوى دوران المصفوفة المتعامدة.

نختار المصفوفة الرباعية الأبعاد التالية:

والتي بعد تحليل قيمها الذاتية، نحصل على مصفوفتي القيم والمتجهات الذاتية:

نذكر أن ترتيب القيم الذاتية في مقذ يوافق ترتيب المتجهات الذاتية في ممذ ونضيف أيضا كملاحظة أن هذا الترتيب يتبّع ترتيب القيم الذاتية من الأعلى إلى الأدنى والجدير بالذكر أن التفرقة التالية مـس = ممذ مقذ ممذ^-1 صالحة لأي ترتيب اختيرة إعتاباطي كان أم منطقي.

نحلل الآن هذه القيم الذاتية ونقوم بحساب مجموعها قبل حساب النسبة المئوية لكلّ واحدة منهم.

نلاحظ أن مجموع النسب يساوي 100٪، مما يعني أن القيم الذاتية تمثل كل الفضاء. وكلّما كانت القيم أعلى، كانت أهميتها أكبر في تمثيل الفضاء.

المتجهات الذاتية تمثل الاتجاهات الأساسية في الفضاء الخطي التي لا يتغير اتجاهها عند تطبيق التحويل الخطي، وهي بذلك تكشف عن أهم المحاور أو الاتجاهات التي يتركز فيها تأثير المصفوفة.

في هذه المرحلة من التحليل، نقوم بحساب حاصل الضرب الخارجي لكل متجه ذاتي بعد ضربه في قيمته الذاتية. ثم نجمع المصفوفات الناتجة تدريجيًا، واحدة تلو الأخرى، إلى أن نُتمّ المتجهات الأربع.

توضح هذه العملية كيف يُسهم كل متجه ذاتي، إلى جانب قيمته الذاتية، في تشكيل المصفوفة الأصلية، مما يُبرز أهمية التحليل الذاتي في فهم البنية الداخلية للمصفوفات.

ولا يقتصر هذا النهج على المصفوفات المتناظرة فقط، كما في المثال أعلاه، إذ يمكن أيضًا تطبيق تحليل القيم والمتجهات الذاتية على المصفوفات غير المتناظرة لتقريب المصفوفة الأصلية بدقة عالية، شريطة أن تكون قابلة للتحليل بهذه الطريقة. وفي كثير من التطبيقات العملية، يكفي استخدام عدد محدود من القيم والمتجهات الذاتية للحصول على تمثيل تقريبي فعّال للمصفوفة الأصلية، مما يجعل هذا التحليل أداة قوية وفعّالة في مجالات متعددة.

في هذا المثال، سنستخدم تحليل القيم الذاتية لتقليل حجم صورة.

لنفترض أن لدينا صورة تمثل بمصفوفة من القيم اللونية. يمكننا تطبيق تحليل القيم الذاتية على هذه المصفوفة لاستخراج أهم الميزات (أو الأنماط) في الصورة.

بعد ذلك، يمكننا استخدام القيم والمتجهات الذاتية لاستخراج تمثيل مضغوط للصورة، مما يقلل من حجم البيانات المطلوبة لتخزين أو بعث الصورة.

إذا أخذنا على سبيل المثال الصورة التالية، وهي صورة ملوّنة ومستطيلة، فسنقوم بتحويلها إلى صورة رمادية مربعة الشكل، حتى نتمكّن من التعامل معها كمصفوفة مربعة، حيث تمثل كلّ قيمة داخل هذه المصفوفة شدة اللون الرمادي (أو السواد) لنقطة معينة في الصورة. بهذه الطريقة، تصبح الصورة عبارة عن فسيفساء زخرفية مكوّنة من عناصر تمثل درجات الإضاءة في كل منطقة، مما يسمح لنا بمعالجتها رياضيًا أو رقميًا.

✵

◉

◉

✵

بعد تطبيق تحليل القيم الذاتية على هذه المصفوفة، يمكننا استخراج القيم الذاتية والمتجهات الذاتية التي تمثل أهم الأنماط في الصورة. باستخدام هذه المعلومات، يمكننا إعادة بناء صورة مضغوطة تحتفظ بأهم التفاصيل، مما يقلل من حجم البيانات المطلوبة لتخزين أو نقل الصورة.

✵

◉

◉

✵

والمنحنى أسفله نرصد تراكم القيم الذاتية. حيث نلاحظ أن تراكم القيم الذاتية الأكبر يحدث في المراحل الأولى، مما يشير إلى أن هذه القيم تمثل المعلومات الأكثر أهمية في الصورة ومنه يمكن التخلّص من نسبة كبيرة من البيانات مع الإحتفاظ بدقّة عالية للصورة من أجل التخزين أو المراسلة الرقمية الفعّالة.

✵

◉

◉

✵

في التطبيقات العملية، تحليل القيم الذاتية والمتجهات الذاتية يُستخدم في مجالات متعددة مثل تحليل البيانات، معالجة الصور، والذكاء الاصطناعي. على سبيل المثال، في تحليل البيانات، يمكن استخدام تحليل القيم الذاتية لتقليل الأبعاد من خلال اختيار القيم الذاتية الأكبر التي تمثل معظم التباين في البيانات.