شبه عكس المصفوفات
عكس المصفوفات المستطيلة
المصفوفة المستطيلة
في الرياضيات، المصفوفة المستطيلة هي مصفوفة تحتوي على عدد مختلف من الصفوف والأعمدة. يمكن أن تكون هذه المصفوفات إما عريضة (عدد الأعمدة أكبر من عدد الصفوف) أو طويلة (عدد الصفوف أكبر من عدد الأعمدة).
المصفوفة العريضة
المصفوفة العريضة هي نوع من المصفوفات المستطيلة حيث يكون عدد الأعمدة أكبر من عدد الصفوف. على سبيل المثال، إذا كانت لدينا مصفوفة تحتوي عل3 صفّين و3 أعمدة، فإنها تعتبر مصفوفة عريضة.
عندما نقوم بإسقاط فضاء ذو بعد أكبر إلى فضاء ذو بعد أقلّ، فإننا نستخدم تحويلة خطية تؤدي غالبًا إلى فقدان أو مزج بعض المعلومات الأصلية. في مثل هذه الحالات، يكون عدد المجهولين في المعادلة أكبر من عدد المعادلات (المعروفات)، مما يجعل من المستحيل عادةً إيجاد حل وحيد ودقيق. هذا النوع من التحويلات شائع في المصفوفات العريضة، حيث لا يمكن استرجاع جميع المعلومات الأصلية بعد الإسقاط، ويصبح من الضروري البحث عن حلول تقريبية أو استخدام مفاهيم مثل شبه عكس المصفوفة.
المصفوفة الطويلة
المصفوفة الطويلة هي نوع من المصفوفات المستطيلة حيث يكون عدد الصفوف أكبر من عدد الأعمدة. على سبيل المثال، إذا كانت لدينا مصفوفة تحتوي على 3 صفوف و عمودين، فإنها تعتبر مصفوفة طويلة.
عندما نقوم بإسقاط فضاء ذي بعد أقل إلى فضاء ذي بعد أعلى باستخدام مصفوفة طويلة، فإننا نضيف أبعادًا جديدة إلى الفضاء المعني، لكننا لا نستطيع أن نملأ الفضاء بالكامل أو ندرج معلومات جديدة فيه. في هذه الحالة، يكون عدد المعروفين في المعادلة أعلى من عدد المجهولين، مما يعني أن هناك العديد من الحلول الممكنة أو قد لا يوجد حل على الإطلاق إذا كانت المعادلات غير متوافقة. هذا النوع من المصفوفات يظهر كثيرًا في مسائل الأنظمة المفرطة التحديد، حيث نحتاج غالبًا إلى إيجاد حل تقريبي (مثل الحل مربّعات الصغرى) بدلاً من حل دقيق وحيد.
شبه عكس المصفوفات
كيف نعكس المصفوفة المستطيلة ؟
شبه عكس المصفوفة هو مفهوم يُستخدم لإيجاد حل تقريبي لمشكلة تتضمن مصفوفة مستطيلة، حيث يكون عدد الصفوف مختلفًا عن عدد الأعمدة. في هذه الحالة، نحتاج إلى استخدام تقنيات خاصة لإيجاد شبه عكس المصفوفة.
مثال تطبيقي
في هذا المثال البسيط نُبيّن المنفعة الظاهرة من استخدام شبه عكس المصفوفة.
نفترض أن لدينا لآلة تتحرّك في غرفة ما ولديها جهاز تستطيع به أن تستشعر نقطة من حائط موجود في الغرفة.
نبني نموذج الحائط رياضيا بمعادلة خط ص = اس + ب
نحتاج إلى نقطتين على الأقل لتحديد معالم الحائط. ولكن بما أن القياسات قد تحتوي على ضوضاء، فإن الاعتماد عليهما فقط قد يؤدي إلى نتائج غير دقيقة.
لذا، نقوم بجمع قياسات متعددة من نقاط مختلفة على الحائط. كل قياس يُعطينا نقطة في الفضاء، ويمكننا تمثيل هذه النقاط في مصفوفة مستطيلة. لا يمكن حساب عكس المصفوفة بالطريقة التقليدية التي سبق تقديمه.
فإذا كانت لدينا مصفوفة تمثل هذه القياسات، فإننا نحتاج إلى إيجاد شبه عكس المصفوفة لنتمكن من حساب المعاملات ا وب بدقة أكبر. باستخدام شبه عكس المصفوفة، يمكننا حساب المعاملات بطريقة تأخذ في الاعتبار جميع القياسات التي قمنا بها، مما يؤدي إلى تقدير أكثر دقة لمعادلة الحائط.
نعرّف شبه عكس المصفوفة بأنه المصفوفة التي تعكس تأثير المصفوفة الأصلية على الفضاء. بمعنى آخر، إذا كانت لدينا مصفوفة مستطيلة مـق، فإن شبه عكسها
هو المصفوفة التي تحقق المعادلة التالية:
نحسب شبه عكس المصفوفة باستخدام الصيغة: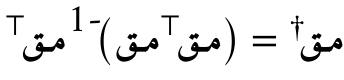
ثم نجد أفضل نموذج للحائط الذي يعتبر كلّ نقط المُستشعرة
.
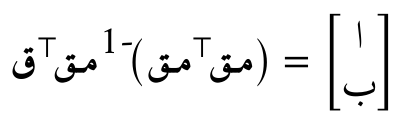في حالات أخرى, إذا كانت المصفوفة عريضة غير طويلة يكون حساب شبه العكس بهذا الشكل حفاظا على أبعاد المصفوفات: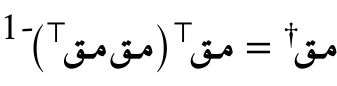
.
الفيديو التالي يعرض تطور نموذج الحائط مع الزيادة في عدد النقاط:
ملحوظة
يمكن تبسيط مفهوم شبه عكس المصفوفة من خلال مثال عددي. لنأخذ العدد أربعة، فعكسه الجبري هو الرُبع. إذا ضربنا أربعة في نفسها ثم أخذنا معكوس الناتج وضربناه مرة أخرى في أربعة، سنحصل على الرُبع. هذه الطريقة الأكثر تعقيدًا لحساب معكوس عدد بسيط تعكس فكرة حساب شبه عكس المصفوفة، حيث يمكن تعميم هذه العملية على المصفوفات لإيجاد شبه عكسها بطريقة مشابهة. فنضرب المصفوفة في نفسها (أو في منقولتها) فنحصل على مصفوفة مربّعة يمكن حساب عكسها فنحسبه ثم نضرب الحاصل في المصفوفة الأصلية التي هي مستطيلة لنحصل على شبع عكس هذه الأخيرة.
