الإشتقاق والتكامل
تعاريف تحليلية
الإشتقاق
تعريف تحليلي للمشتقة
في علم التفاضل والتكامل، المشتقة هي مقياس لمعدل تغير الدالة بالنسبة إلى متغيرها المستقل. تعبر المشتقة عن ميل المنحنى عند نقطة معينة، وتساعد في فهم كيفية تغير الكمية مع مرور الوقت أو مع تغير متغير آخر.
نعرّف رياضيا عملية الاشتقاق كالتالي:
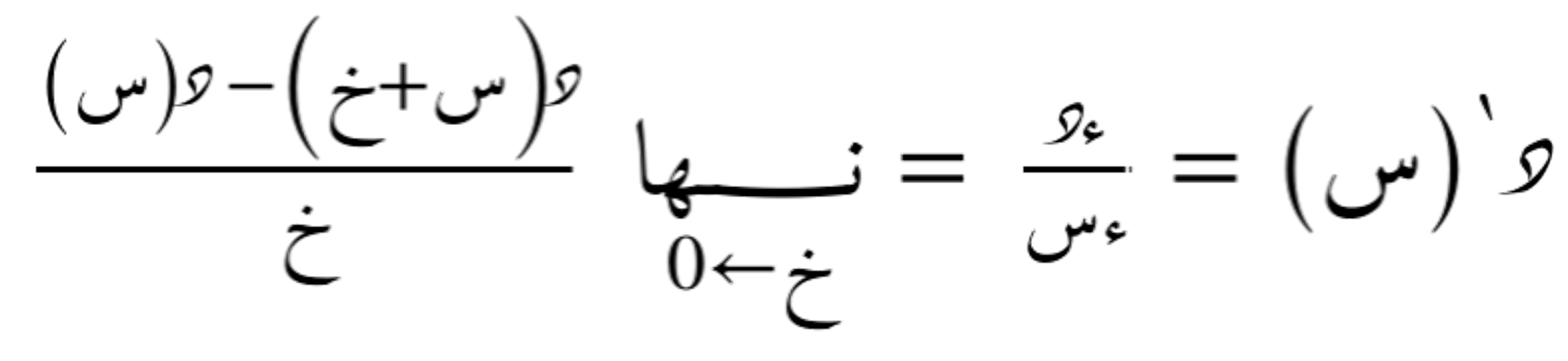
و منه المُشتقة الثانية يُرمز لها ب:
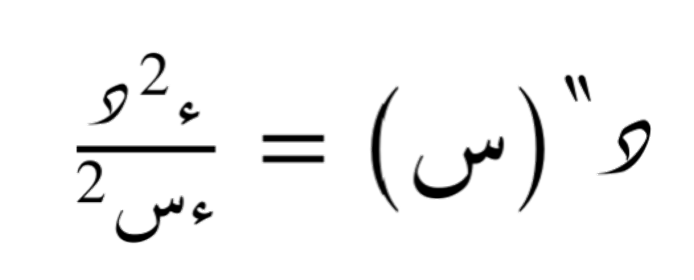
المشتقة الأولى تعبر عن معدل التغير اللحظي للدالة، بينما المشتقة الثانية تعبر عن معدل تغير المشتقة الأولى، مما يساعد في فهم تسارع أو تباطؤ التغير في الدالة.
و أيضا المُشتقة الثالثة يُرمز لها ب:
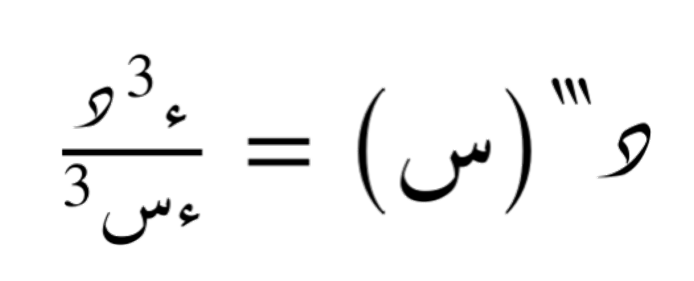
تطبيق بسيط في الإشتقاق
في هذا القسم، سنقوم بتطبيق بسيط على مفهوم المشتقة. سنأخذ دالة بسيطة ونحسب مشتقتها. لنأخذ الدالة التالية كمثال: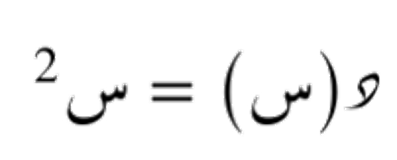
ثم نحسب مشتقتها باستخدام تعريف المشتقة:
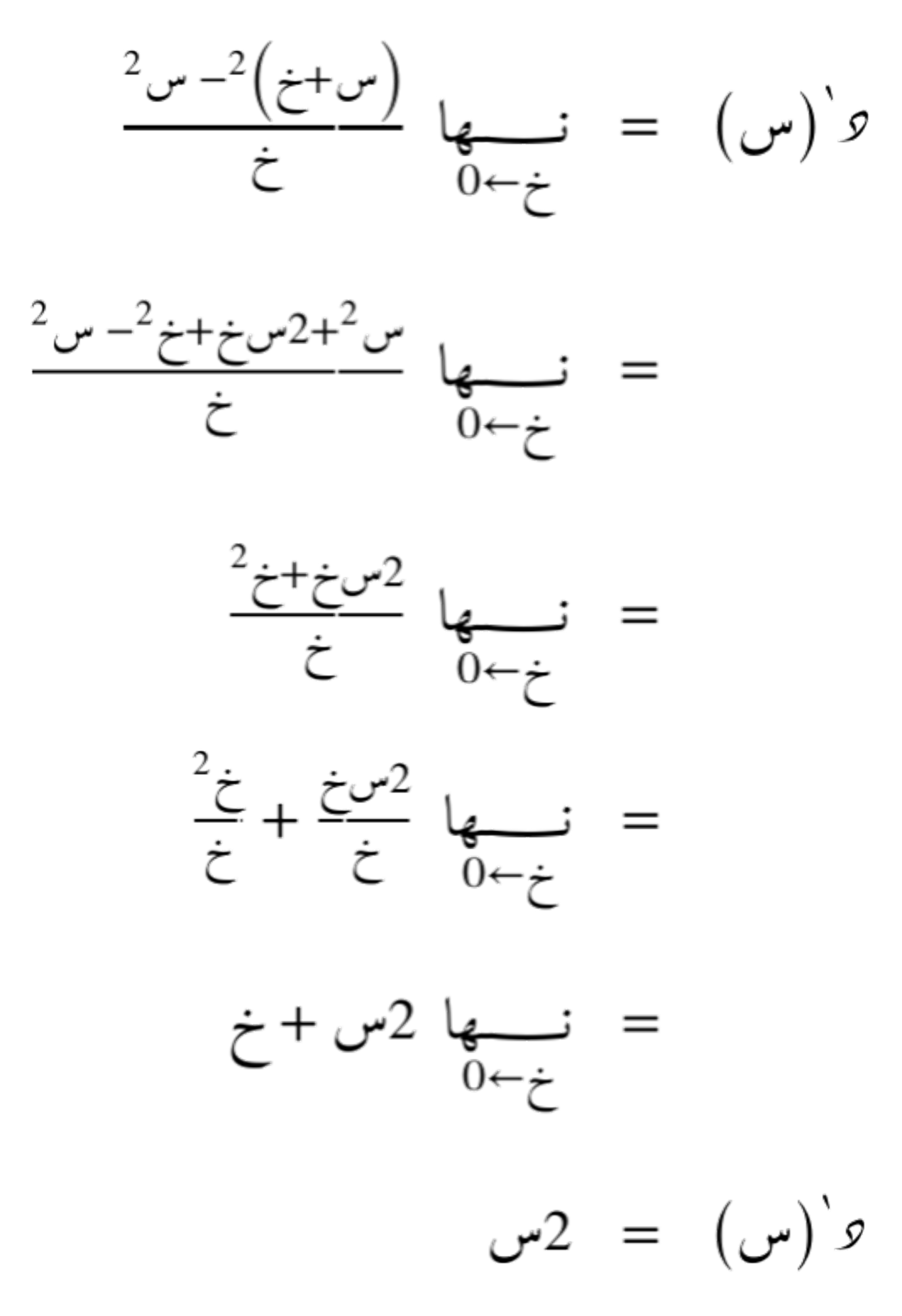
مشتقات دوال معروفة
فيما يلي أهم قواعد مشتقات الدوال المعروفة التي تُستخدم كثيرًا في التفاضل ويمكن حسابها بنفس طريقة المثال السابق.
الدوال الحدودية
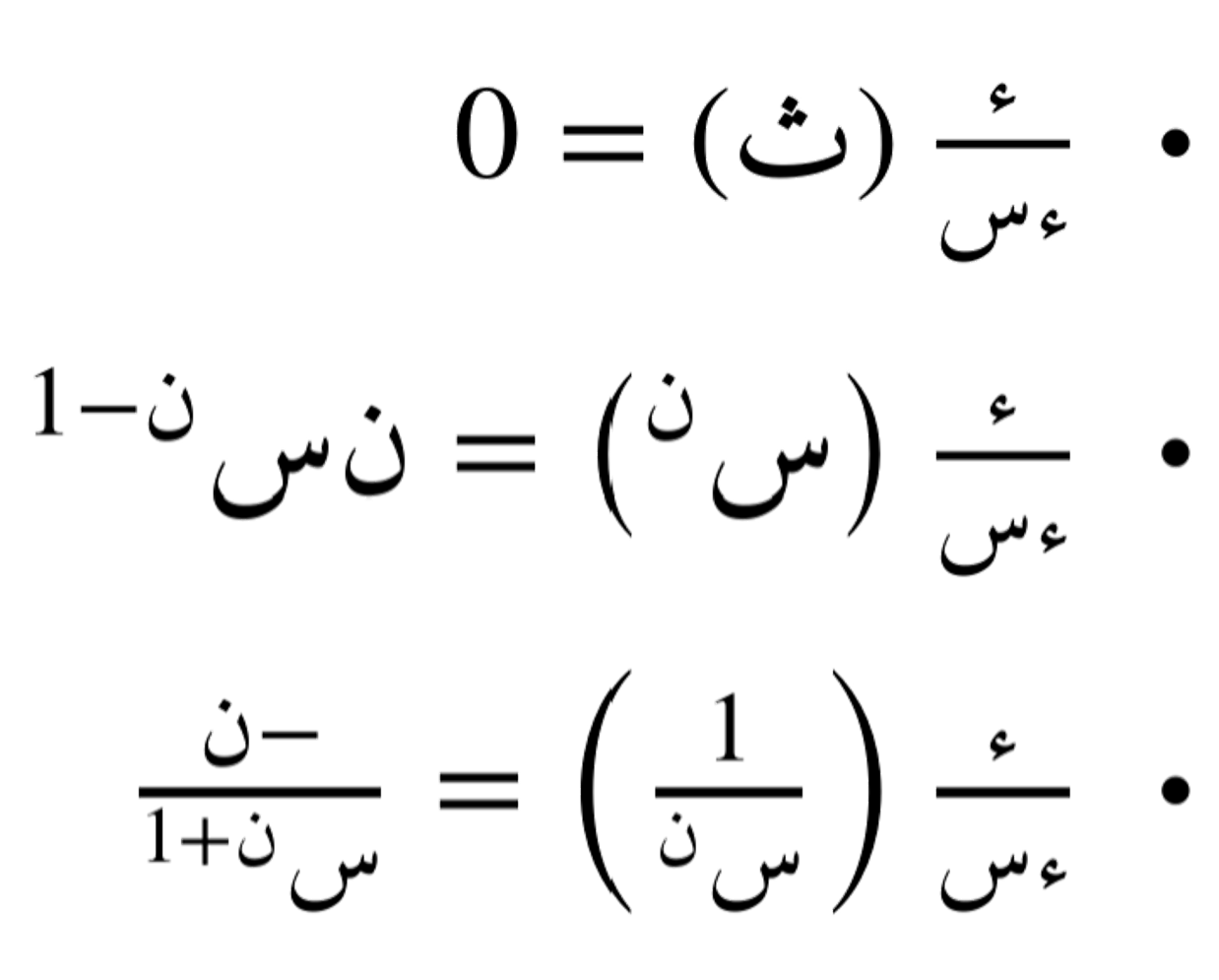
الدوال الجيبية

الدوال الأسية واللوغاريتمية
الدالة الأسية هس هي الدالة الوحيدة التي مشتقتها تساوي نفسها. أي أن مشتقة هس هي أيضًا هس. هذه الخاصية تجعل الدالة الأسية مهمة جدًا في الرياضيات والعلوم، حيث تظهر في العديد من التطبيقات التي تتعلق بالنمو أو التغير المستمر.
ومن جهة أخرى، اللوغاريتم يُعرّف رياضيًا بأنه الدالة التي مشتقتها هي 1\س، وذلك لأن هذه الخاصية تجعل اللوغاريتم مناسبًا لوصف النمو البطيء والتغير النسبي، ولهذا السبب تُستخدم هذه الدالة في العديد من التطبيقات الرياضية والفيزيائية.
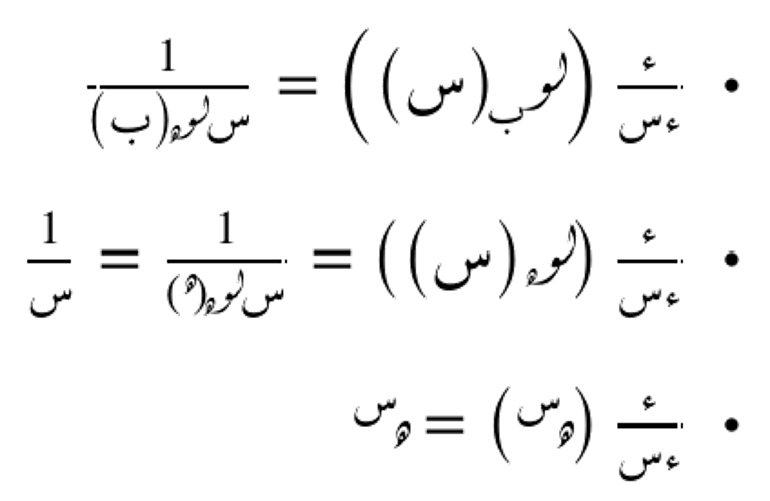
دالة 1\س ليست كثيرة حدود من الدرجة الصفرية لأن س يقترب من الصفر يجعلها غير معرفة، وبالتالي لا يمكننا التعامل معها كما نتعامل مع الدوال البسيطة؛ لهذا نلجأ إلى تعريف دالة اللوغاريتم التي تربط بين المشتقة 1\س وتراكم التغيرات، مما يسمح بفهم هذه الدالة بشكل أدق وامتدادها إلى مجالات أوسع.
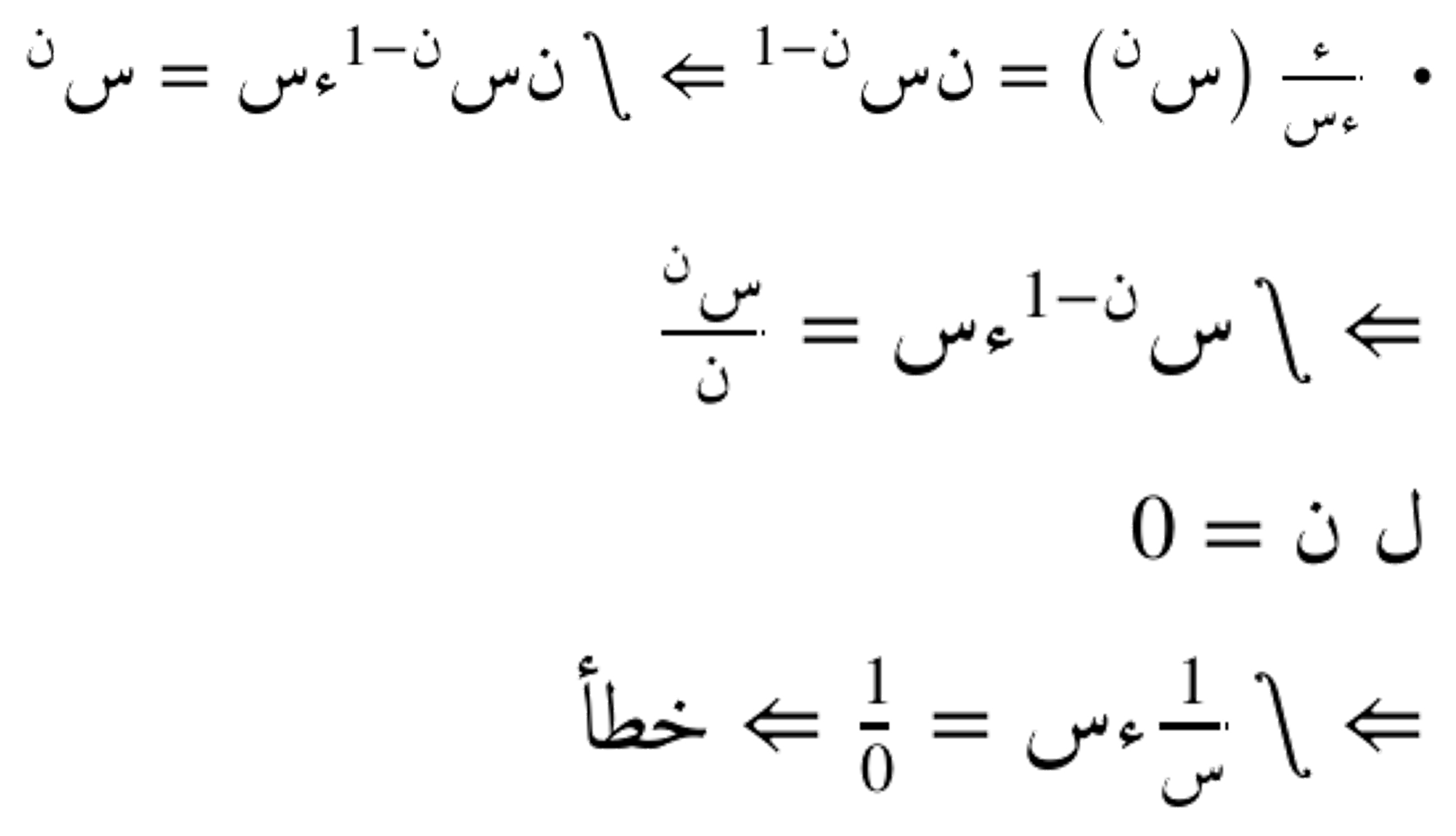
قواعد الإشتقاق عامة
هناك بعض القواعد العامة التي يمكن استخدامها لحساب مشتقات الدوال بشكل أسرع وأسهل. هذه القواعد تشمل:
- قاعدة الجمع: مشتقة مجموع دالتين هي مجموع مشتقات كل منهما.
- قاعدة الطرح: مشتقة فرق دالتين هي فرق مشتقات كل منهما.
- قاعدة الضرب: مشتقة حاصل ضرب دالتين هي: (مشتقة الأولى × الثانية) + (الأولى × مشتقة الثانية).
- قاعدة القسمة: مشتقة حاصل قسمة دالتين هي: (مشتقة البسط × المقام - البسط × مشتقة المقام) ÷ (المقام^2).
- قاعدة السلسلة: مشتقة دالة مركبة هي: مشتقة الدالة الخارجية مضروبة في مشتقة الدالة الداخلية.
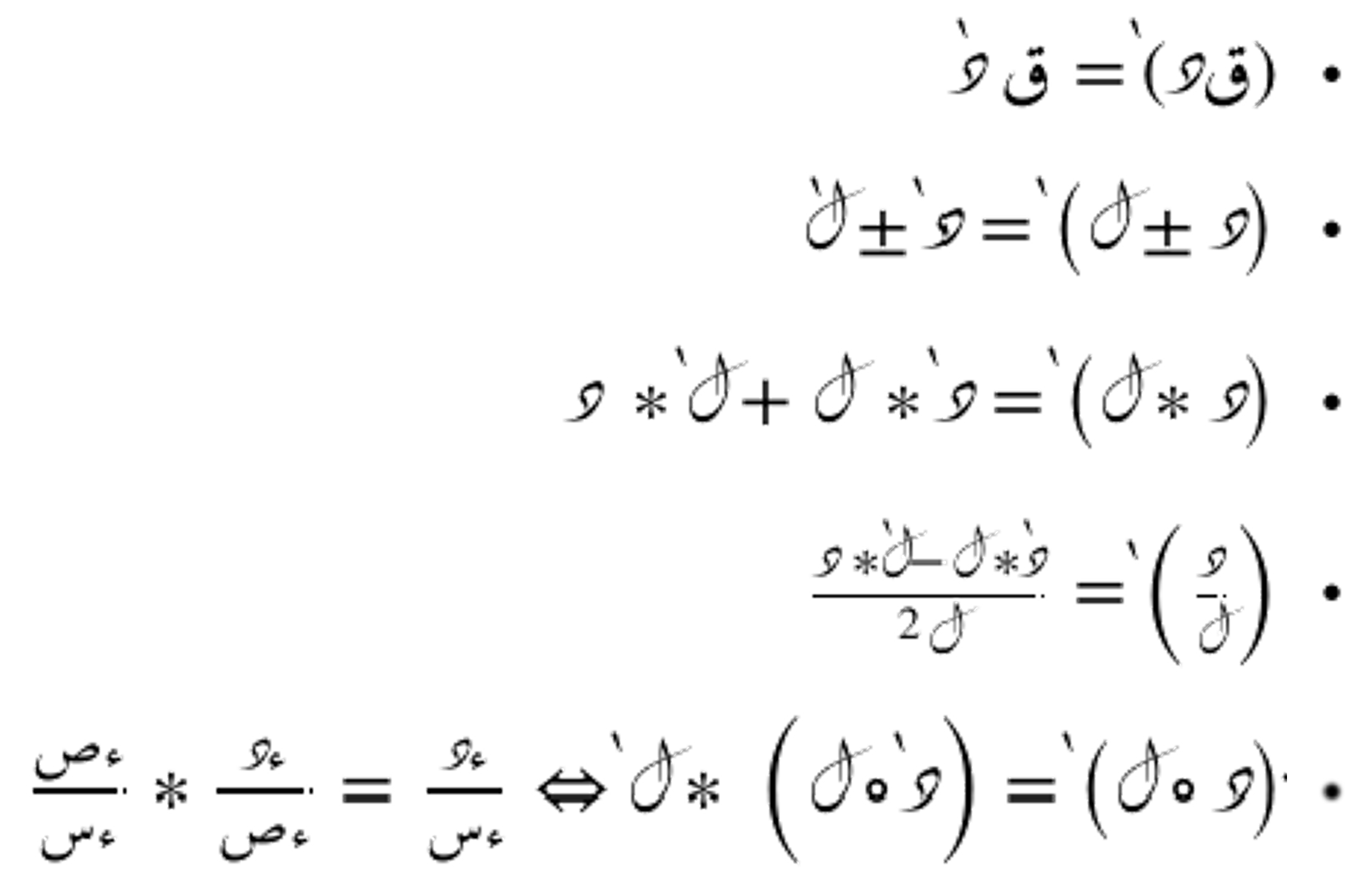
التكامل
تعريف تحليلي للتكامل
التكامل هو العملية العكسية للمشتقة، وهو يُستخدم لحساب المساحة تحت منحنى الدالة أو إيجاد التراكم الكلي لكمية ما. يمكن اعتباره طريقة لجمع القيم الصغيرة التي تعبر عن التغير التدريجي للحصول على الكمية الكلية.
لِتَكُن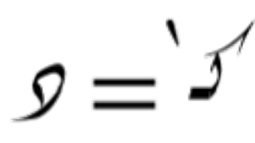 لدينا
لدينا
التكامل المحدد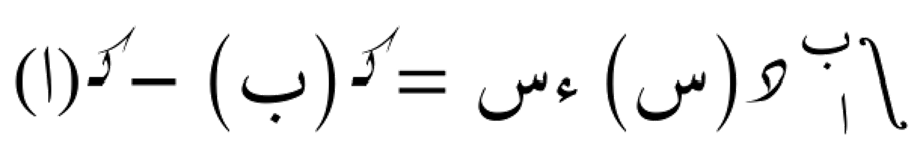
التكامل المحدد هو طريقة لحساب التغير الكلي أو المساحة تحت منحنى دالة ما بين نقطتين محددتين. نحدد نقطتي البداية والنهاية، ثم نحسب مجموع القيم الصغيرة للدالة بين هاتين النقطتين. الناتج يعبر عن مقدار التغير الكلي أو المساحة ضمن الفترة المحددة.
التكامل غير المحدد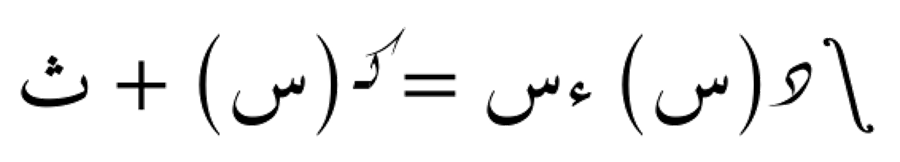
التكامل غير المحدد هو عملية حسابية تهدف إلى إيجاد الدالة الأصلية لدالة معينة. لا يتضمن هذا النوع من التكامل حدودًا محددة، بل يعبر عن مجموعة من الدوال التي تختلف فقط في ثابت التكامل. يُستخدم التكامل غير المحدد لاستعادة الدالة الأصلية التي تم اشتقاقها.
تطبيق بسيط في التكامل
في هذا القسم، سنقوم بتطبيق بسيط على مفهوم التكامل. سنأخذ دالة بسيطة ونحسب تكاملها. لنأخذ الدالة التالية كمثال: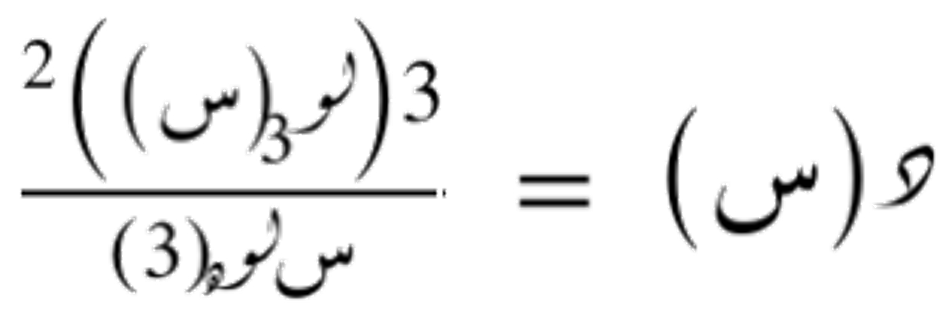
ثم نحسب تكاملها باستخدام تعريف التكامل:

نعرّف دالتين ل و كـ التان تبسّطان صياغة التكامل المُرادُ حِسابُه.
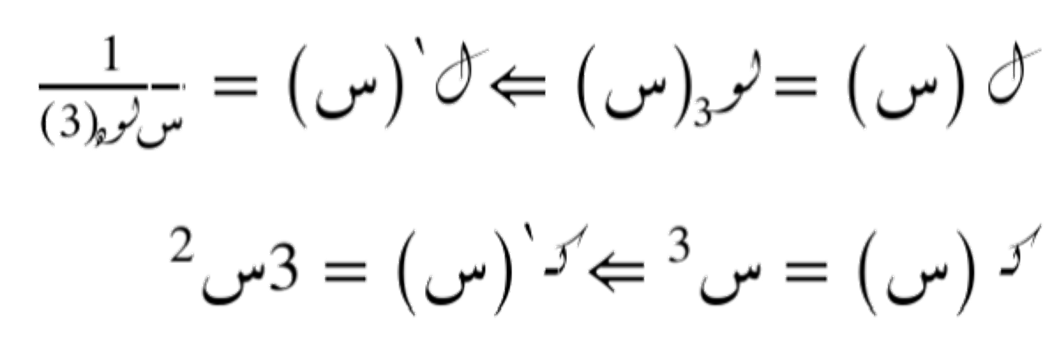
التكامل غير المحدد للدالة إذن هو (مع ثابت مُنعدم):
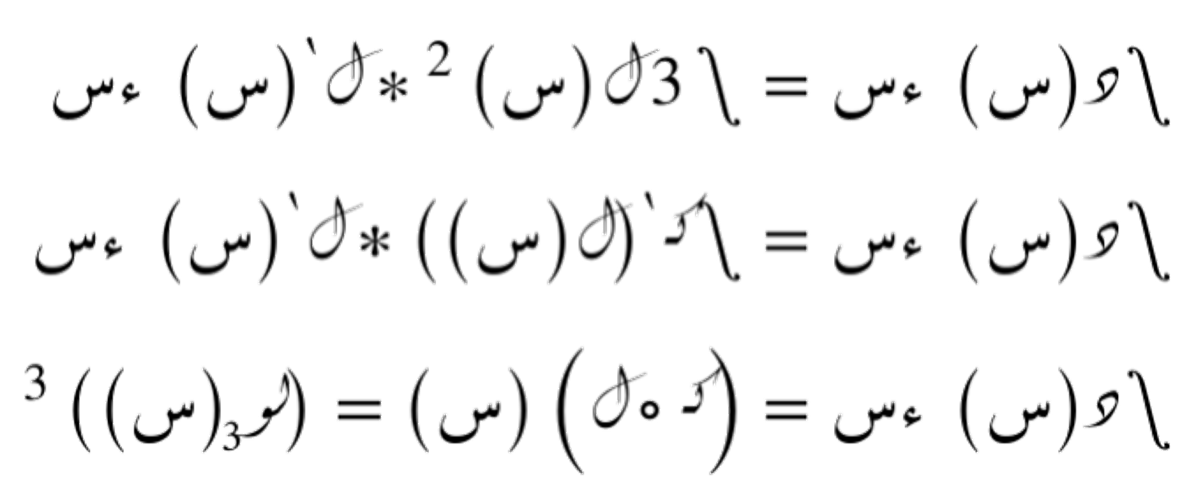
التكامل بالأجزاء
هذا المثال مهّد لنا الطريق لِفهم مفهوم التكامل بالأجزاء.
التكامل بالأجزاء هو تقنية تُستخدم لتبسيط حساب التكاملات التي يصعب حسابها مباشرة. تعتمد هذه التقنية على قاعدة التكامل بالأجزاء، والتي تنص على أن:
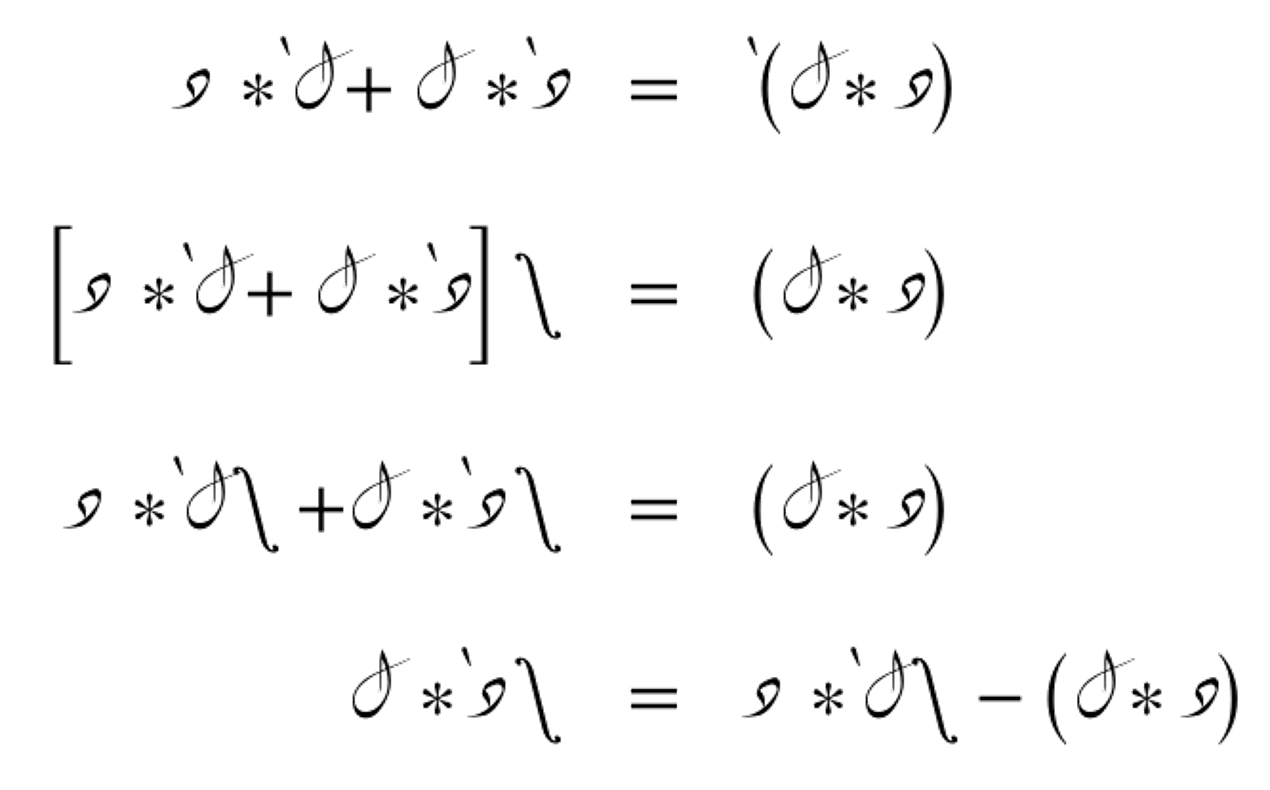
لنأخذ مثالاً على التكامل بالأجزاء. لنحسب التكامل التالي:
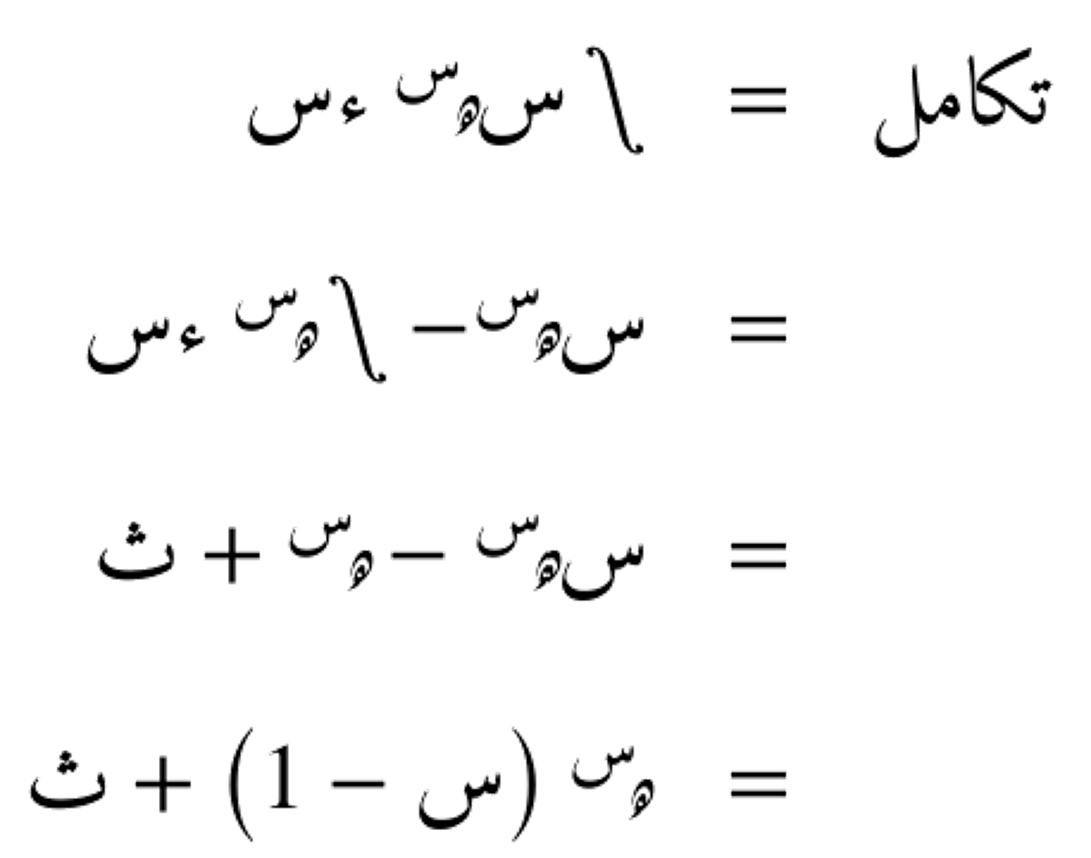
الإشتقاق والتكامل: العلاقة بينهما
أسئلة للتدبّر
في هذا القسم، سنطرح بعض الأسئلة التي تساعد على فهم العلاقة بين الاشتقاق والتكامل بشكل أعمق. هذه الأسئلة تهدف إلى تحفيز التفكير النقدي حول كيفية ارتباط هاتين العمليتين الرياضيتين ببعضهما البعض.
- لماذا الاشتقاق هو عكس التكامل؟
- لماذا المساحة تحت منحنى دالة ما هو مُؤشر لتغيّر دالّتُها المُتكاملة؟
- لماذا تغيّر دالة ما هو المساحة تحت منحنى دالّتها المُشتقة؟
لماذا الاشتقاق هو عكس التكامل؟
لأن الاشتقاق يقيس معدل تغير الدالة، بينما التكامل يجمع هذه التغيرات لاستعادة الدالة الأصلية (مع ثابت). إذا اشتققنا دالة ثم قمنا بتكامل الناتج، نعود للدالة الأصلية تقريبًا.
لماذا المساحة تحت منحنى دالة ما هو مُؤشر لتغيّر دالّتُها المُتكاملة؟
لأن التكامل يحسب مجموع القيم الصغيرة للدالة عبر فترة معينة، وهو ما يمثل المساحة تحت المنحنى. هذه المساحة تعبر عن التغير الكلي للكمية التي تصفها الدالة.
لماذا تغيّر دالة ما هو المساحة تحت منحنى دالّتها المُشتقة؟
إذا كانت لدينا دالة تصف كمية متغيرة، فإن مشتقتها تمثل معدل التغير اللحظي. جمع هذه المعدلات (أي التكامل) عبر فترة معينة يعطينا التغير الكلي، وهو ما تمثله المساحة تحت منحنى المشتقة.





