الإشتقاق التحليلي
متعدد المتغيّرات
الإشتقاق الجزئي
في هذا الدرس، سوف نتناول مفهوم الإشتقاق الجزئي، وهو مفهوم أساسي في حساب التفاضل والتكامل متعدد المتغيرات. الإشتقاق الجزئي يُستخدم لحساب معدل التغير لدالة متعددة المتغيرات بالنسبة لأحد متغيراتها مع اعتبار المتغيرات الأخرى ثابتة.
على سبيل المثال، إذا كانت لدينا دالة ثلاثية الأبعاد مثل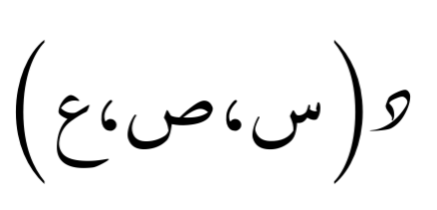
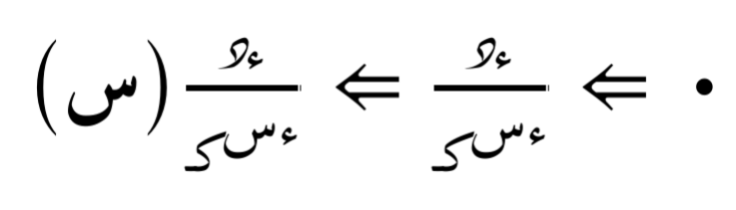
فإن الإشتقاق الجزئي بالنسبة لـ س أو ص أو ع يُعطى بالعلاقة التالية:
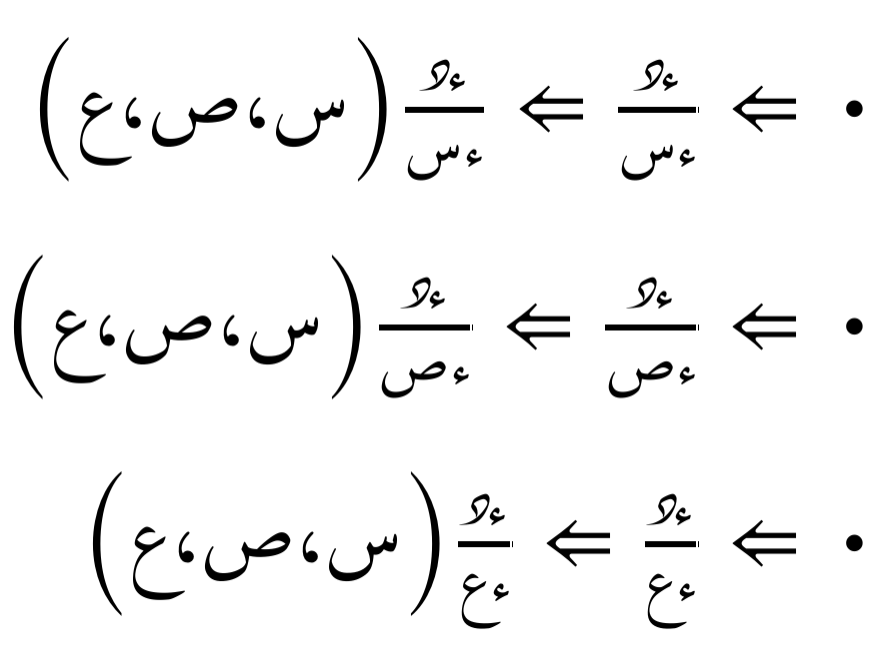
المُشتقات الجزئية للدالة الأصلية هِي أيضا دوالّ بدلالة نفس المتغيّرات.
مثال لدالة متعددة المتغيرات
لنفترض أن لدينا الدالة التالية: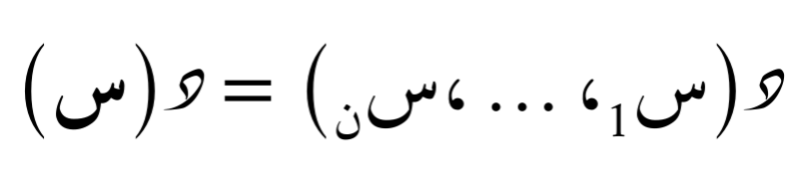
لحساب المشتقات الجزئية لهذه الدالة، نقوم بتطبيق قواعد الإشتقاق الجزئي كما يلي بالنسبة لكلّ مُتغيّر:
مُتجه التدرّج
مُتجه التدرّج هو مفهوم يُستخدم لوصف اتجاه ومعدل التغير لدالة متعددة المتغيرات في نقطة معينة. يُمثل مُتجه التدرّج مجموعة من المشتقات الجزئية للدالة بالنسبة لكل متغير.
إذا كانت لدينا دالة ثلاثية الأبعاد مثل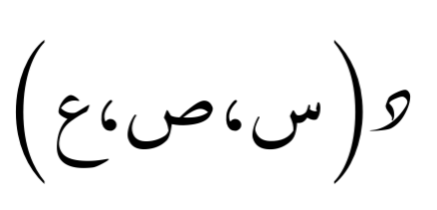
فإن مُتجه التدرّج لهذه الدالة يُعطى بالعلاقة التالية:
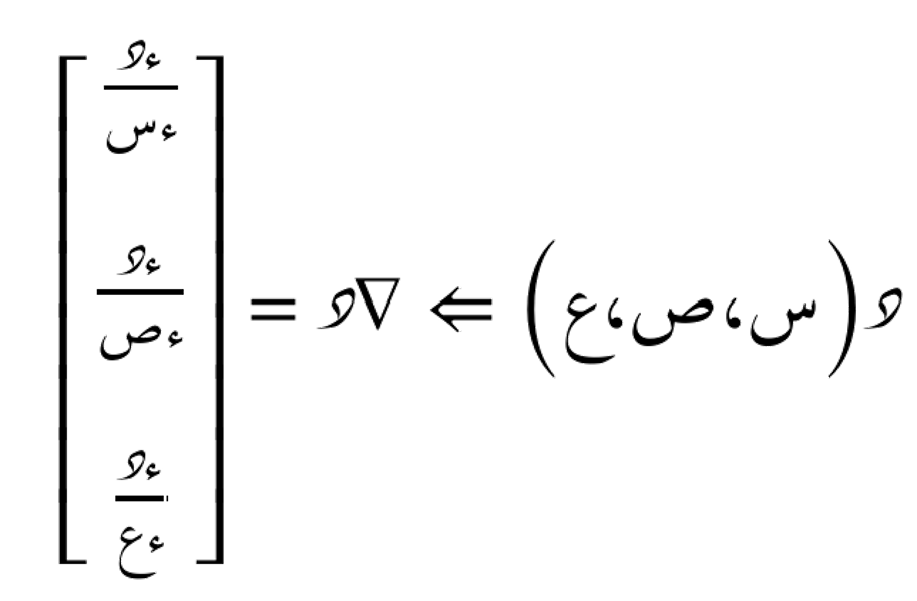
خصائص مُتجه التدرّج
لمُتجه التدرّج عدة خصائص مهمة، منها:
- يُشير مُتجه التدرّج دائمًا في اتجاه أكبر معدل تغير للدالة.
- طول مُتجه التدرّج يُعطي معلومات عن مقدار هذا التغير.
- إذا كانت الدالة ثابتة، فإن مُتجه التدرّج يكون صفرًا.
مثال لدالة متعددة المتغيرات
لنفترض أن لدينا الدالة التالية: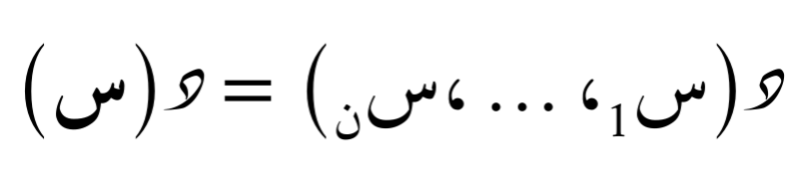
نبني مُتجه التدرّج كما يلي:
قاعدة الإشتقاق المُتسلسل
قاعدة الإشتقاق المُتسلسل تُستخدم لحساب مشتقات الدوال التي تعتمد على دوال أخرى. هذه القاعدة تُعتبر أداة قوية في حساب التفاضل والتكامل متعدد المتغيرات.
نعتبر لدينا الدالة المُركّبة د(س(ز))
لحساب مشتقة هذه الدالة بالنسبة لـ ز، نستخدم قاعدة الإشتقاق المُتسلسل كما يلي:
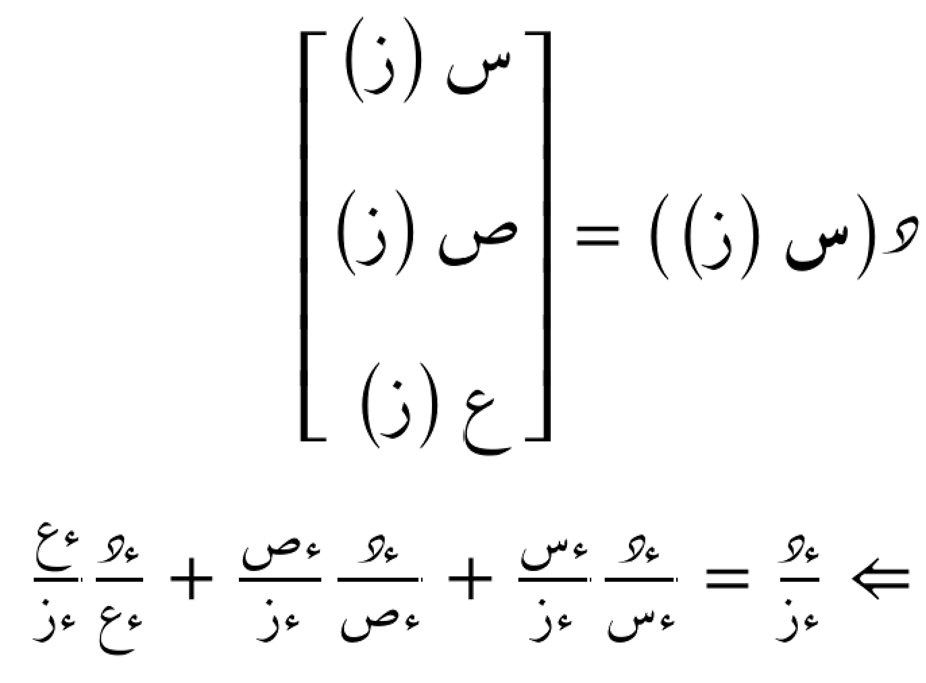
مثال دالة متعددة المتغيرات
لنفترض أن لدينا الدالة التالية: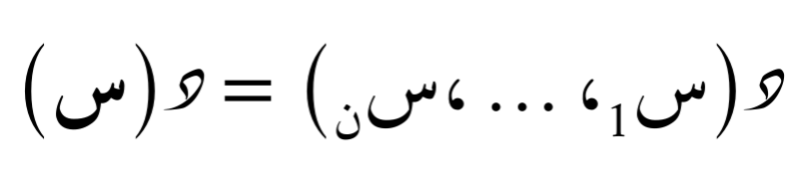
لحساب مشتقة هذه الدالة بالنسبة لـ ز، نطبق قاعدة الإشتقاق المُتسلسل كما يلي:
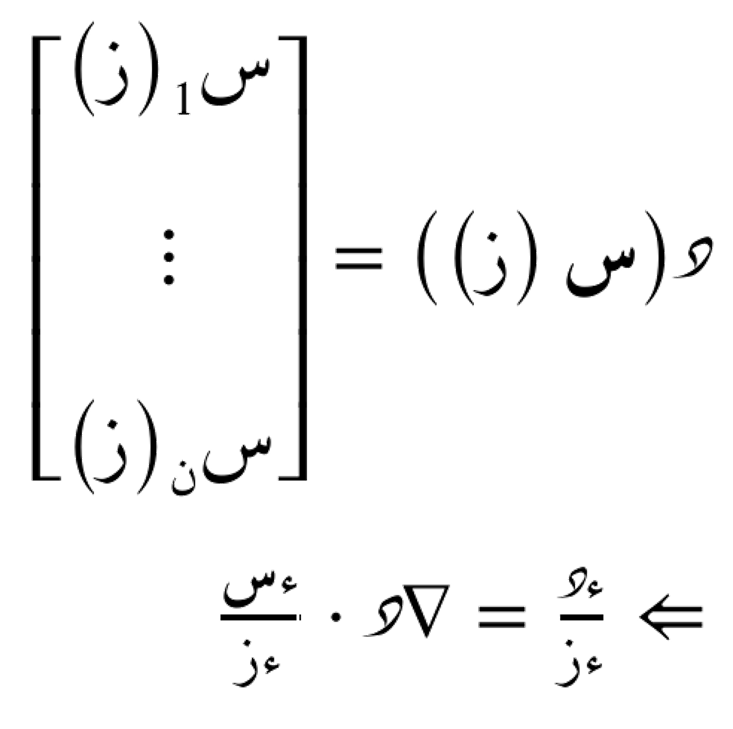
وبذلك نحصل على مشتقة الدالة بالنسبة لـ ز. حيث أن المشتقة بالنسبة لـ ز تكون بدلالة متجه التدرّج.
المشتقات الجزئية الثانية
المشتقات الجزئية الثانية هي مشتقات المشتقات الجزئية الأولى. تُستخدم هذه المشتقات لتحليل سلوك الدوال متعددة المتغيرات بشكل أعمق.
أمثلة عامّة
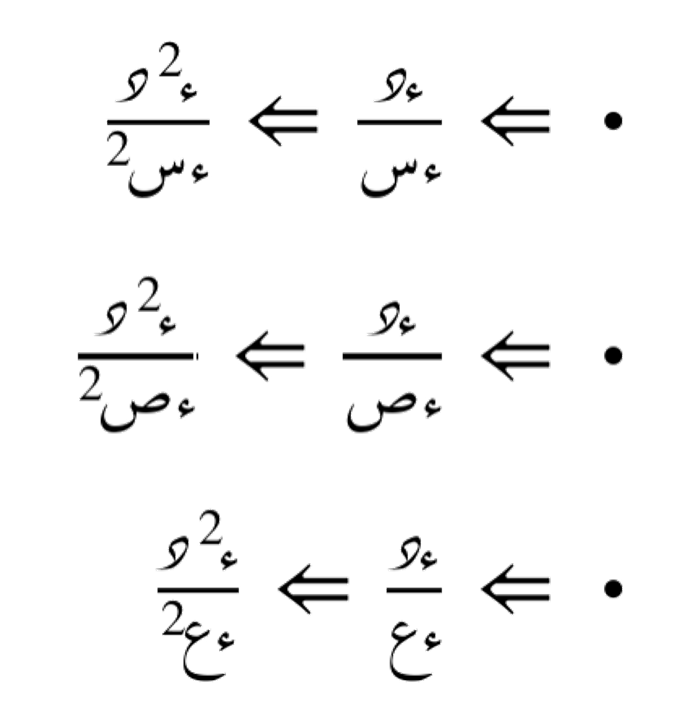
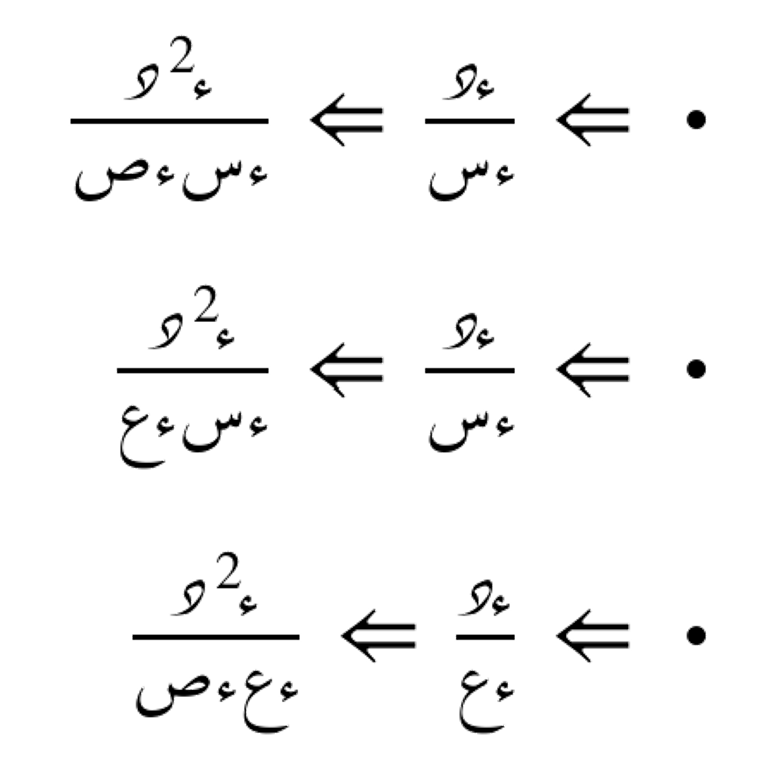
المشتقات الجزئية الثانية تُعطي معلومات عن تقعر الدالة وسلوكها حول النقاط الحرجة. إذا كانت المشتقات الجزئية الثانية موجبة، فإن الدالة تكون مقعرة لأعلى، وإذا كانت سالبة، فإن الدالة تكون مقعرة لأسفل.
المشتقات الجزئية الثالثة
المشتقات الجزئية الثالثة هي مشتقات المشتقات الجزئية الثانية. تُستخدم هذه المشتقات لتحليل سلوك الدوال متعددة المتغيرات بشكل أعمق.
أمثلة عامّة
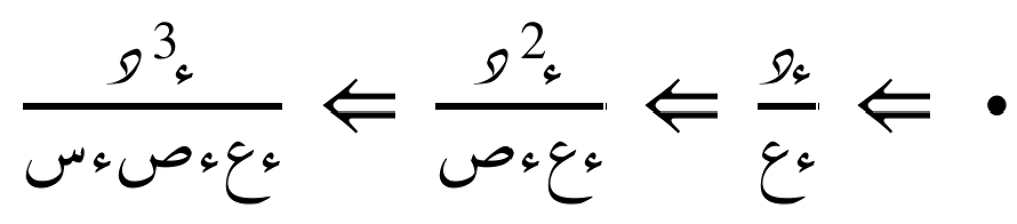
عادةً يمكن تبديل ترتيب الاشتقاق الجزئي (أي اشتقاق الدالة أولاً بالنسبة لمتغيّر ثم بالنسبة لآخر أو العكس) إذا كانت الدالة مستمرة وقابلة للاشتقاق بشكل كافٍ في المنطقة المدروسة. في هذه الحالة، تكون المشتقات الجزئية المختلطة متساوية، أي أن: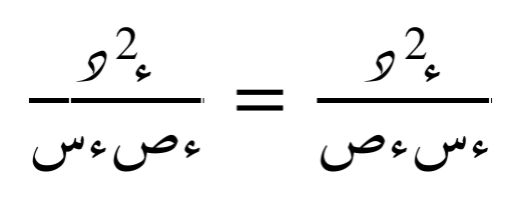
أما إذا لم تكن الدالة مستمرة أو غير قابلة للاشتقاق بشكل كافٍ، فقد لا يكون تبديل الترتيب صحيحًا دائمًا وهذا يتنطبق أيضا على مُشتقات جُزئية أعلى كالثالثة والرابعة إلخ...
مصفوفة المشتقات الجزئية الثانية
مصفوفة المشتقات الجزئية الثانية تُستخدم لوصف سلوك الدوال متعددة المتغيرات بشكل أعمق. هذه المصفوفة تُعتبر أداة قوية في تحليل الدوال وتطبيقات الرياضيات التطبيقية.
إذا كانت لدينا دالة ثلاثية الأبعاد مثل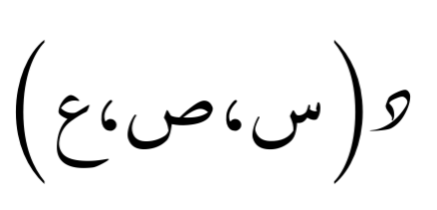
فإن مصفوفة المشتقات الجزئية الثانية لهذه الدالة تُعطى بالعلاقة التالية:
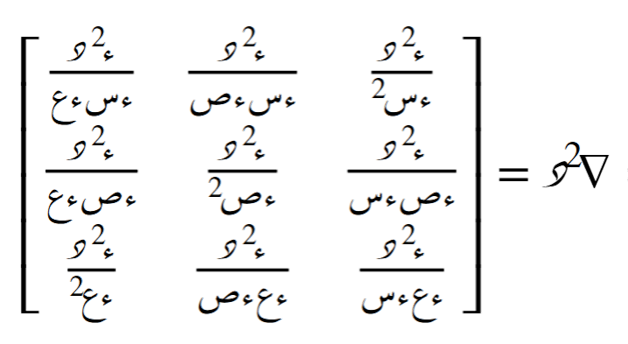
خصائص مصفوفة المشتقات الجزئية الثانية
لمصفوفة المشتقات الجزئية الثانية عدة خصائص مهمة، منها:
- تُعتبر مصفوفة متماثلة إذا كانت المشتقات الجزئية المختلطة متساوية.
- تُستخدم في تحليل الاستقرار في الأنظمة الديناميكية.
- تساعد في تحديد النقاط الحرجة وسلوك الدالة حولها.
مثال لدالة متعددة المتغيرات
لنفترض أن لدينا الدالة التالية: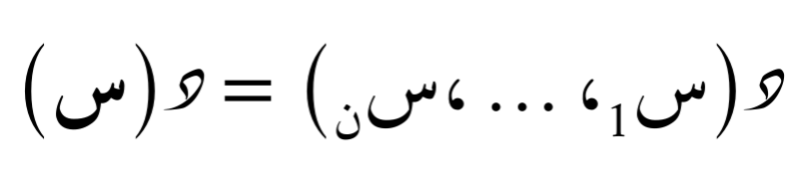
لحساب مصفوفة المشتقات الجزئية الثانية لهذه الدالة، نقوم بتطبيق قواعد المشتقات الجزئية كما يلي:
