التحليل المُتجهي
يُستخدم مؤثرات التباعد والتدوير في العديد من التطبيقات، مثل تحليل الحقول الفيزيائية (مثل الحقول الكهربائية والمغناطيسية)، ودراسة تدفق السوائل والغازات، وفي مجالات أخرى تتعلق بالفيزياء والهندسة. هذه المؤثرات تعتمد على مصفوفة التدرّج التي سنستعرضها أوّلا.
مصفوفة التدرّج
مصفوفة التدرّج تسمى أيضا المصفوفة اليَعقوبية. في التحليل المتجهي، مصفوفة التدرّج هي أداة رياضية تُستخدم لوصف كيفية تغير دالة متعددة المتغيرات في نقاط مختلفة من فضاء المتغيرات. تُعتبر مصفوفة التدرّج جزءًا أساسيًا من دراسة التفاضل في الفضاءات المتعددة الأبعاد، حيث تسمح بفهم كيفية تغير الدالة في اتجاهات مختلفة. مصفوفة التدرّج تُستخدم في العديد من التطبيقات، مثل تحسين الدوال، تحليل البيانات، والفيزياء.
لِتكن الدالة: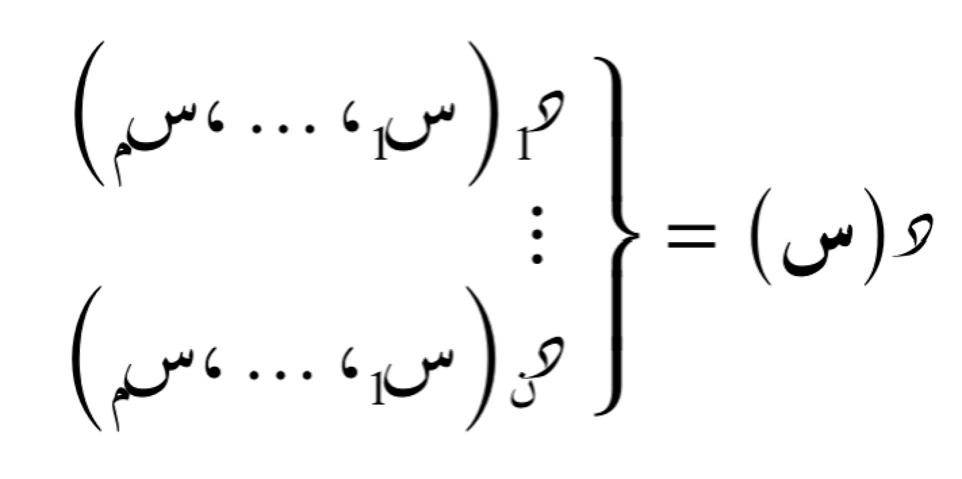
مصفوفة التدرّج لهذه الدالة هي:
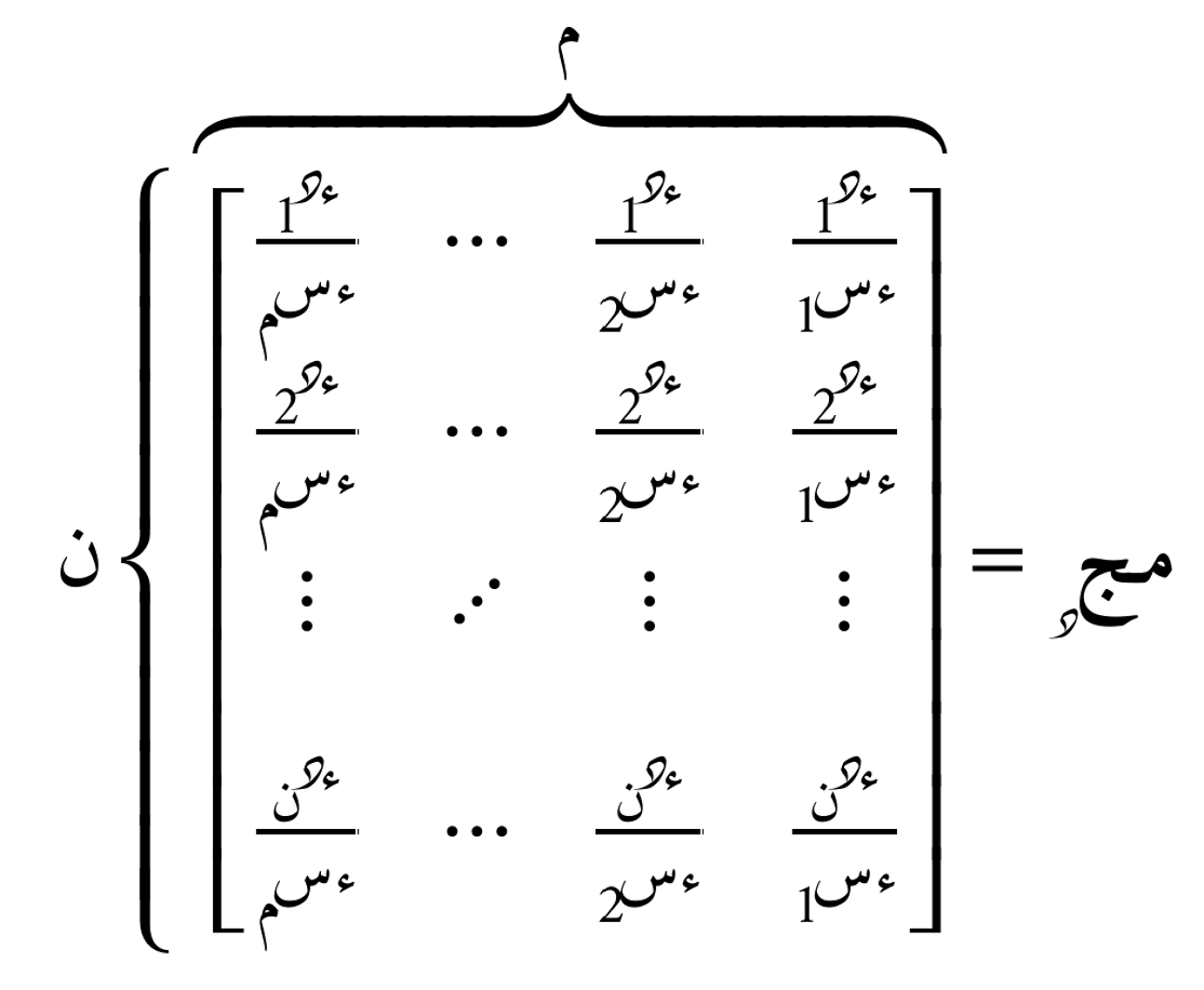
حيث يُمكن أيضا إعادة صياغة العِبارة بدلالة مُتجهات التدرج:
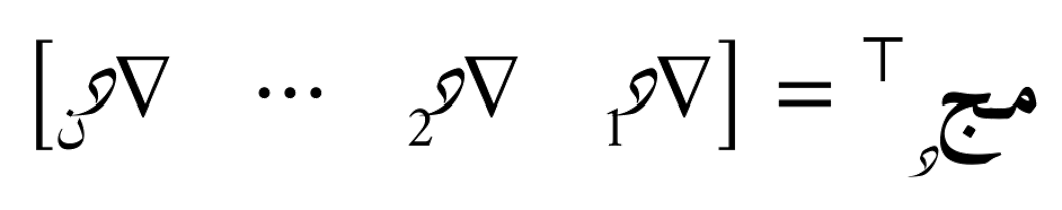
مثال
لِتكن الدالة:
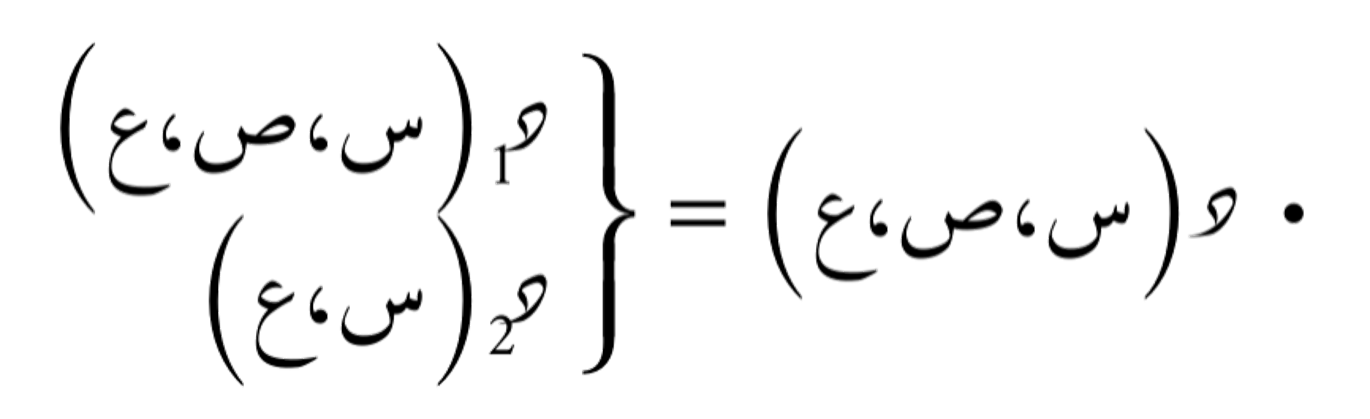
مصفوفة التدرّج لهذه الدالة هي:
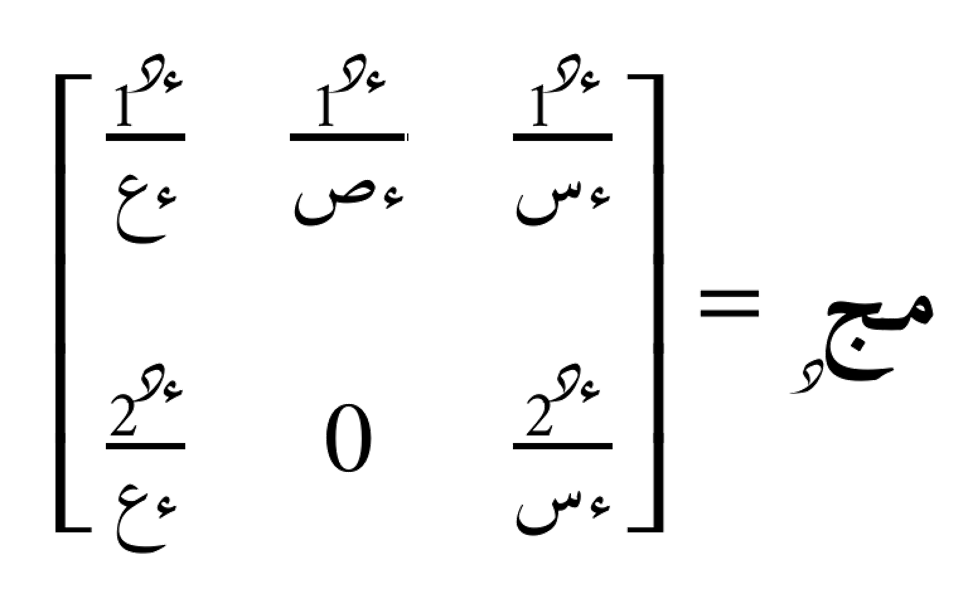
مُؤتر التباعد
مؤثر التباعد هو أثر مصفوفة التدرّج، أي مجموع عناصر القطر الرئيسي للمصفوفة عندما تكون مربعة (أي عندما تكون الدالة معرفة من فضاء بعده ن إلى نفس الفضاء). يُستخدم مؤثر التباعد لقياس مدى انتشار أو تباعد متجهات الحقل عند نقطة معينة في الفضاء. إذا كان التباعد موجبًا في نقطة ما، فهذا يعني أن الحقل "ينتشر" أو "يتباعد" من تلك النقطة، وإذا كان سالبًا فهو "يتجمع" أو "يتقارب" نحوها.
لِتكن الدالة:![]()
مؤتر التباعد لهذه الدالة هو:
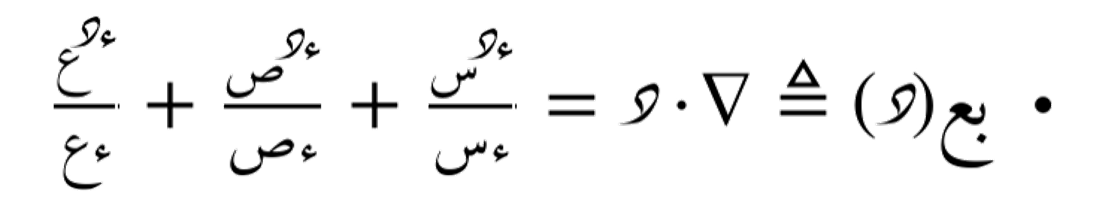
مؤتر التباعد في الفضاءات المتعددة الأبعاد
يُمكن تعميم مؤثر التباعد للفضاءات ذات الأبعاد الأعلى كما يلي:
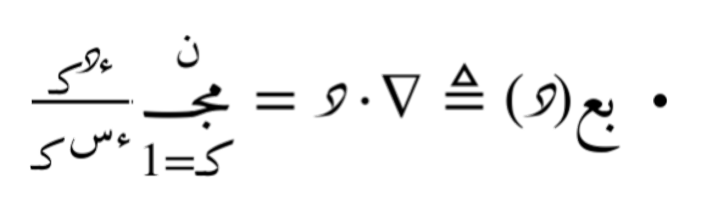
وتقييمه عند النقطة س0:
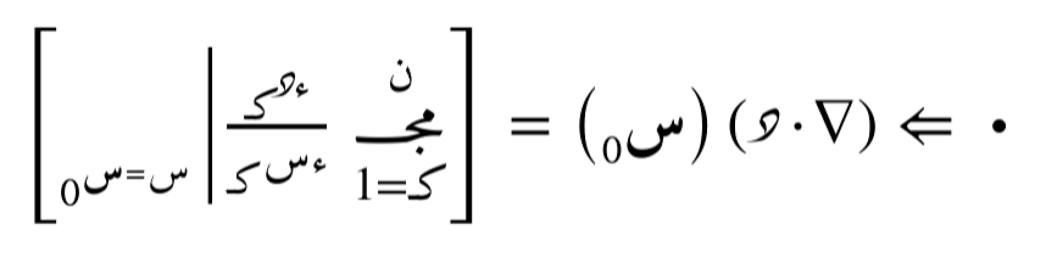
أمثلة على مؤتر التباعد
نستعرض في هذا القسم أمثلة توضيحية لمؤثر التباعد في فضاءات مختلفة الأبعاد.
مثال ثنائي الأبعاد
نعتبر الحقل المتجهي التالي في الفضاء الثنائي الأبعاد:
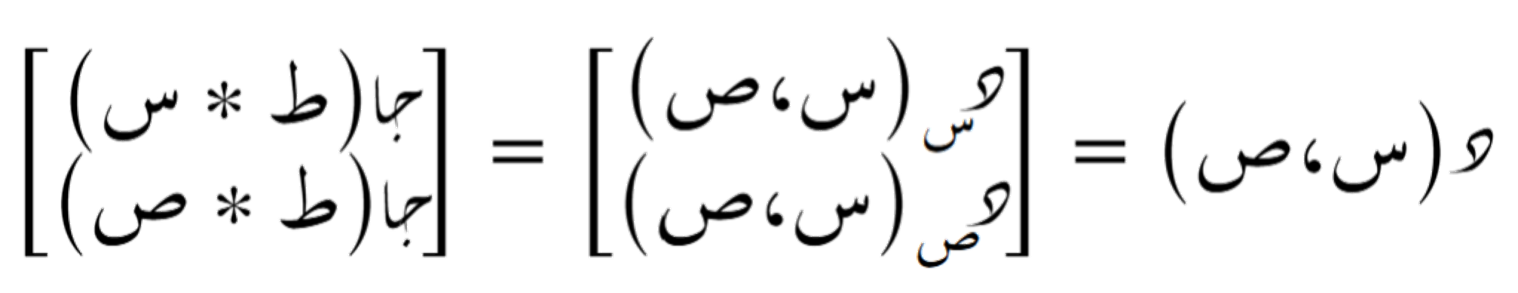
عند تمثيل هذا الحقل المتجهي مع مؤثر التباعد، نحصل على الشكل التالي:
مثال ثلاثي الأبعاد
نعتبر الحقل المتجهي التالي في الفضاء الثلاثي الأبعاد:
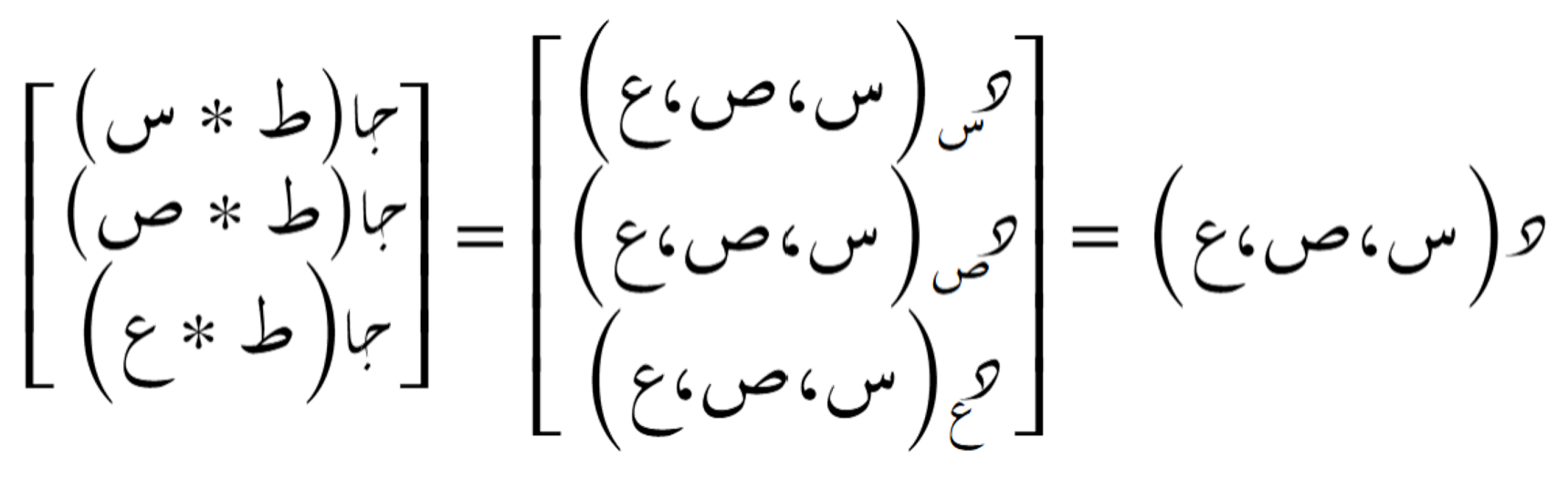
عند تمثيل هذا الحقل المتجهي مع مؤثر التباعد، نحصل على التمثيل التالي:
مُؤتر التدوير
مؤثر التدوير يُستخدم لقياس مدى دوران أو إلتواء متجهات الحقل عند نقطة معينة في الفضاء. إذا كان التدوير موجبًا في نقطة ما، فهذا يعني أن الحقل "يدور" أو "يلتف" حول تلك النقطة، وإذا كان سالبًا فهو "يتوقف" أو "يتراجع" عنها.
لِتكن الدالة:![]()
مؤتر التدوير لهذه الدالة هو:
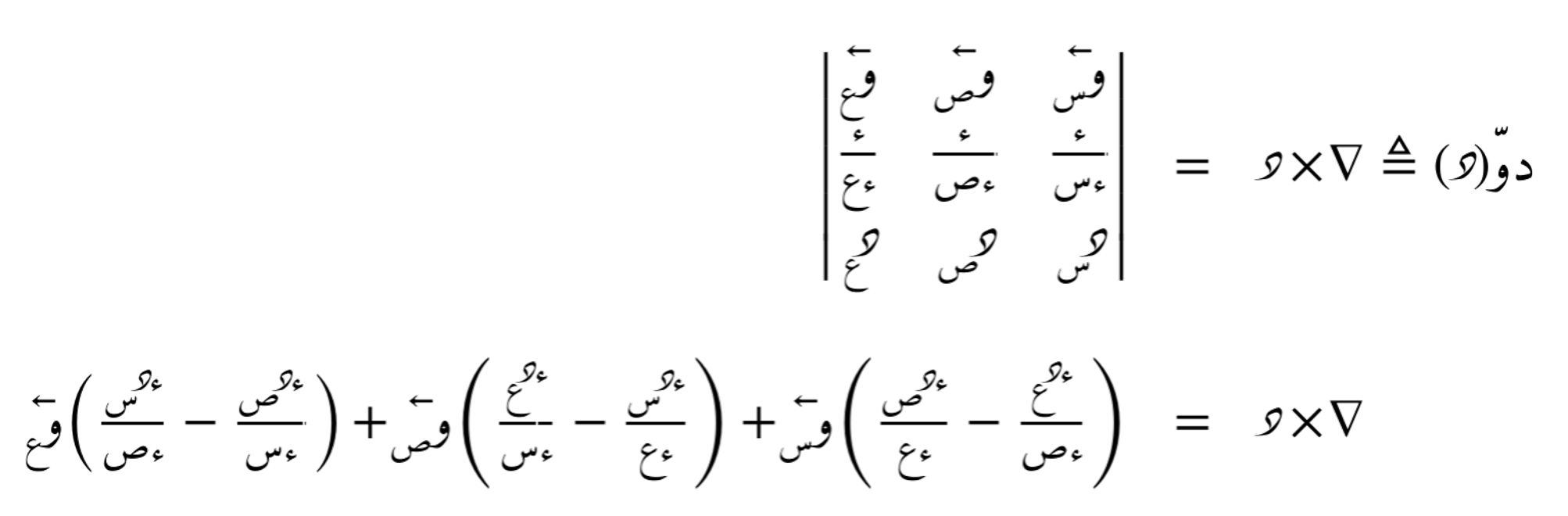
وتقييمه عند النقطة س0:
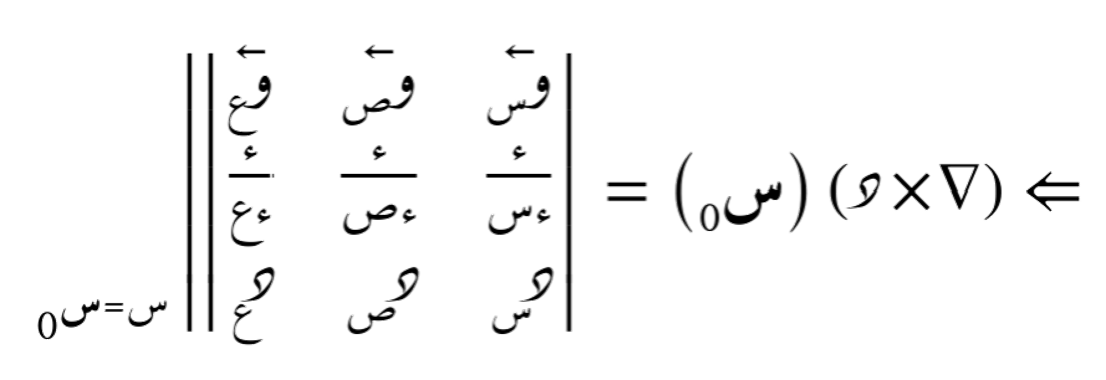
أمثلة على مؤتر التدوير
نستعرض في هذا القسم أمثلة توضيحية لمؤثر التدوير في فضاءات مختلفة الأبعاد.
مثال ثنائي الأبعاد
نعتبر الحقل المتجهي التالي في الفضاء الثنائي الأبعاد:
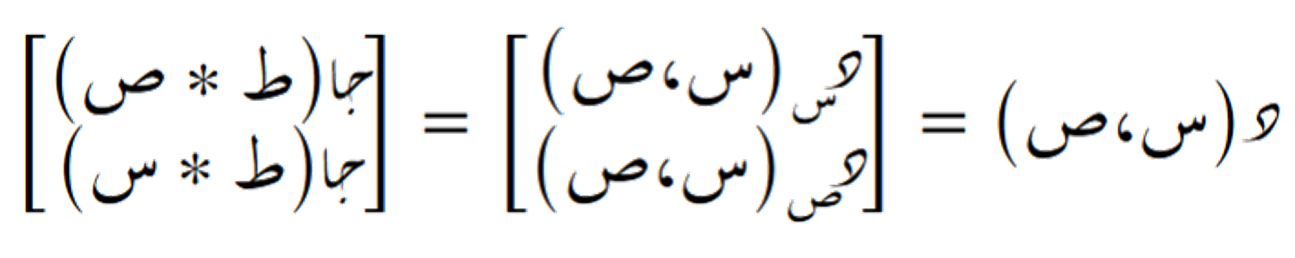
عند تمثيل هذا الحقل المتجهي مع مؤثر التدوير، نحصل على الشكل التالي:
مثال ثلاثي الأبعاد
نعتبر الحقل المتجهي التالي في الفضاء الثلاثي الأبعاد:
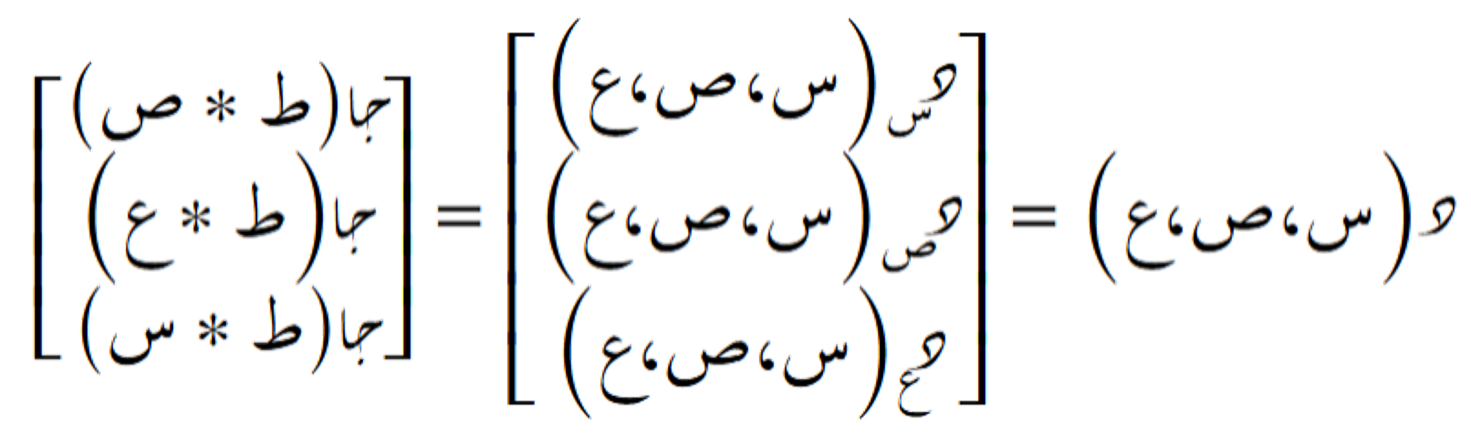
عند تمثيل هذا الحقل المتجهي مع مؤثر التدوير، نحصل على التمثيل التالي:



