التكامل التحليلي
متعدد المتغيّرات
التكامل متعدد المتغيّرات هو فرع من فروع حساب التفاضل والتكامل الذي يتعامل مع الدوال التي تعتمد على أكثر من متغيّر. في هذه الفقرة، سنستعرض بعض الأمثلة للتكامل متعدد المتغيّرات.
لتكن دالة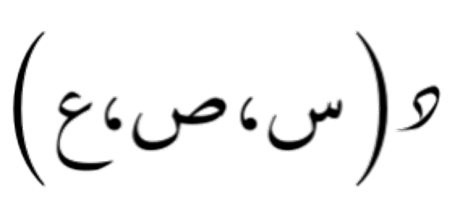
تكامل أحادي المتغيّر
التكامل أحادي المتغيّر هو عملية حسابية تُستخدم لتكامل الدوال التي تعتمد على متغيّر واحد. يُمثّل التكامل المساحة تحت منحنى الدالة في المستوى الثنائي الأبعاد.
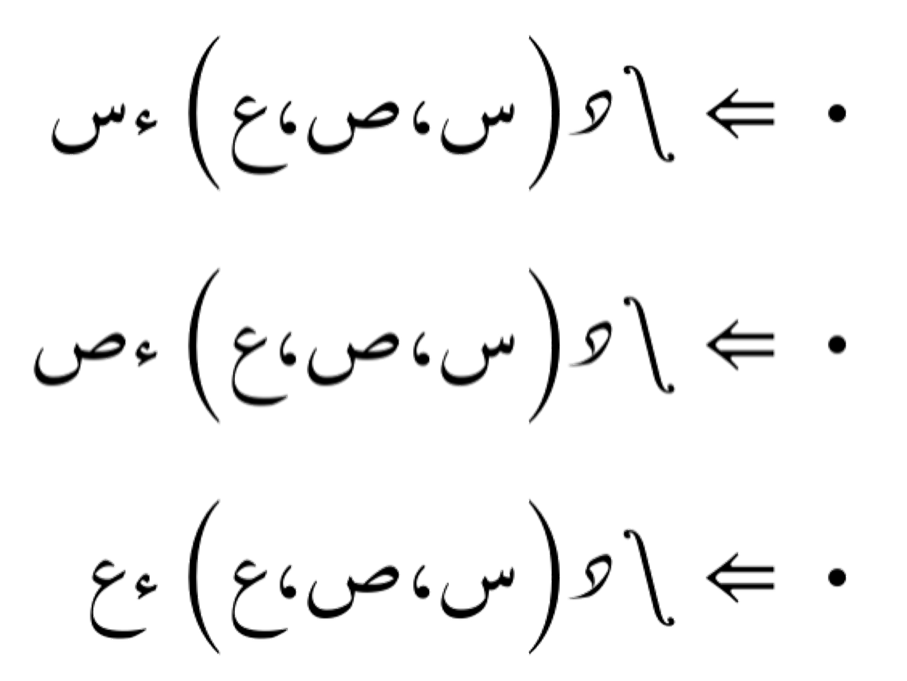
تكامل ثنائي
التكامل الثنائي هو عملية حسابية تُستخدم لتكامل الدوال التي تعتمد على متغيّرين. يُمثّل التكامل الثنائي المساحة تحت سطح الدالة في فضاء ثلاثي الأبعاد.
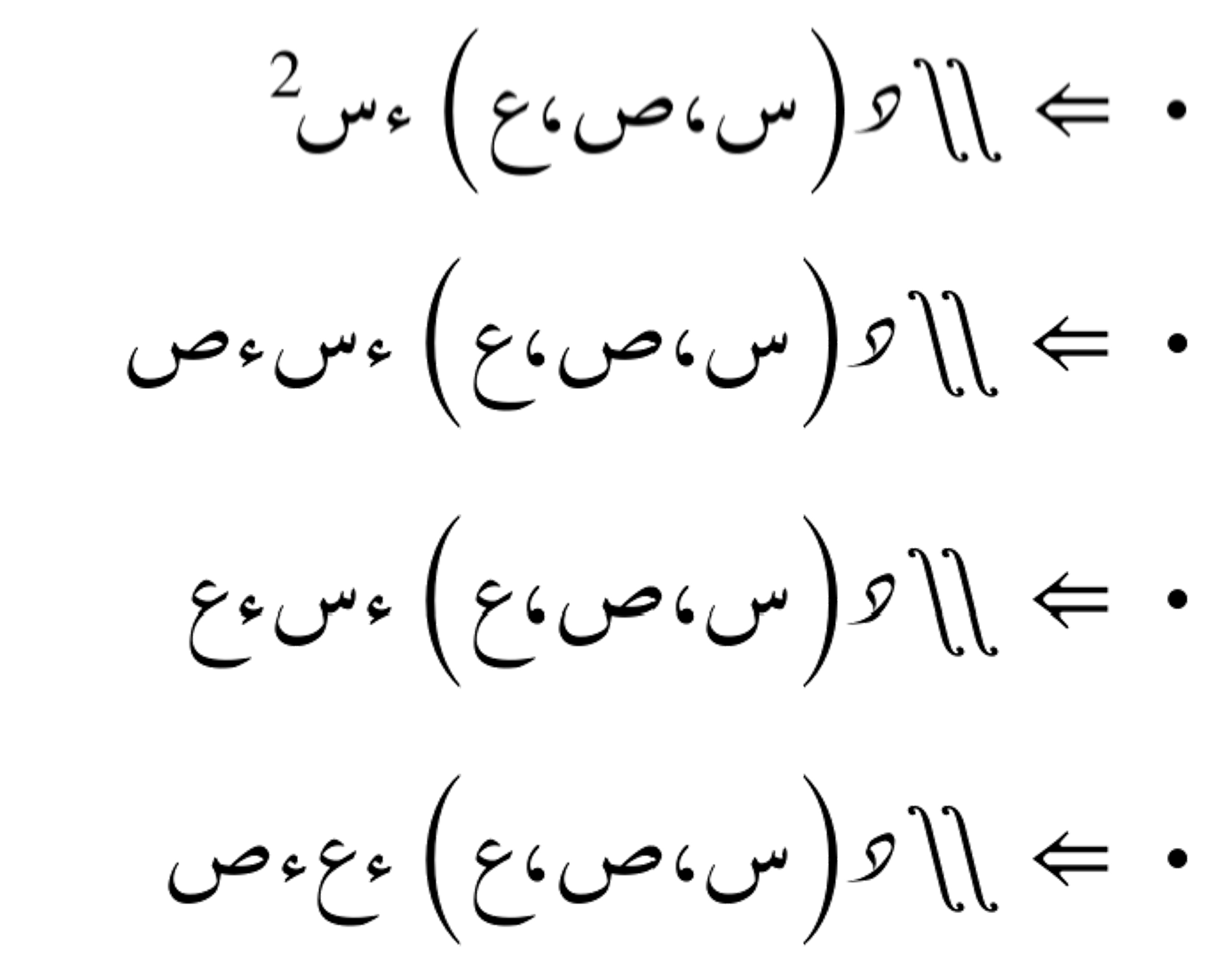
تكامل ثلاثي
التكامل الثلاثي هو عملية حسابية تُستخدم لتكامل الدوال التي تعتمد على ثلاثة متغيّرات. يُمثّل التكامل الثلاثي الحجم تحت سطح الدالة في فضاء رباعي الأبعاد.

تكامل رباعي
التكامل الرباعي هو عملية حسابية تُستخدم لتكامل الدوال التي تعتمد على أربعة متغيّرات. يُمثّل التكامل الرباعي الحجم تحت سطح الدالة في فضاء خماسي الأبعاد.
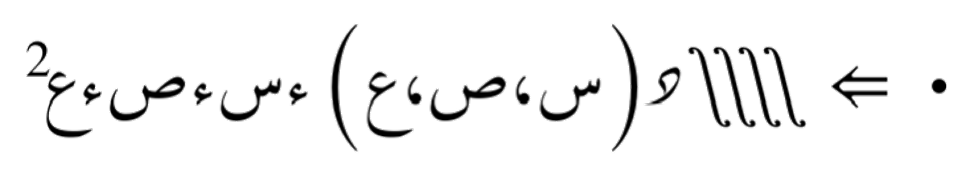
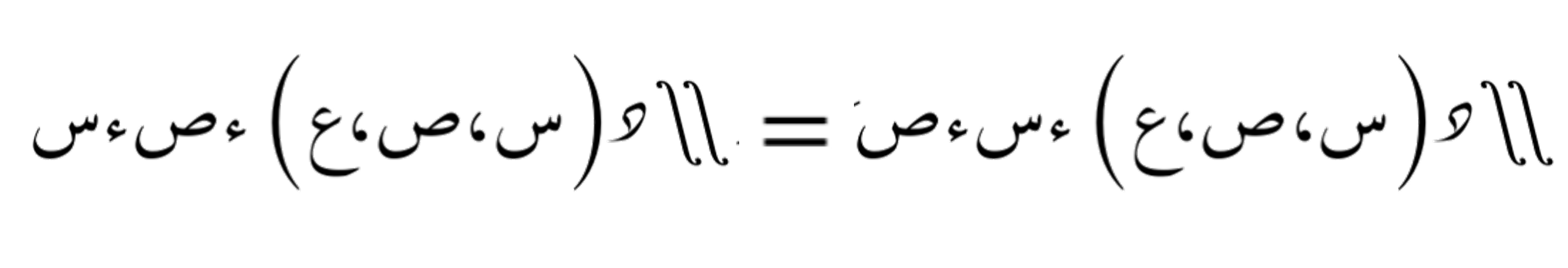 في بعض الحالات الخاصة، قد لا يكون تبديل الترتيب صحيحًا دائمًا، وهذا ينطبق أيضًا على التكاملات الأعلى مثل الثلاثية والرباعية إلخ... دراسة هذه الإمكانية تعتمد على شروط معينة للدالة التي يتم تكاملها، مثل كونها مستمرة أو قابلة للتفاضل في المنطقة المحددة.
في بعض الحالات الخاصة، قد لا يكون تبديل الترتيب صحيحًا دائمًا، وهذا ينطبق أيضًا على التكاملات الأعلى مثل الثلاثية والرباعية إلخ... دراسة هذه الإمكانية تعتمد على شروط معينة للدالة التي يتم تكاملها، مثل كونها مستمرة أو قابلة للتفاضل في المنطقة المحددة.