الإشتقاق رقمي
أحادي المتغيّر
الإشتقاق الرقمي
الإشتقاق الرقمي هو طريقة لتقريب المشتقات باستخدام القيم العددية. هذه الطريقة مفيدة عندما لا يمكن حساب المشتقة بشكل تحليلي أو عندما تكون البيانات متاحة فقط في شكل نقاط وليس كعبارة دالة كاملة.
في هذه الفقرة، سنستعرض كيفية حساب المشتقات الرقمية باستخدام طرق مختلفة، مثل طريقة الفرق الأمامي وطريقة الفرق الخلفي وطريقة الفرق المركزي.
طرق الإشتقاق الرقمي
هناك عدة طرق لحساب المشتقات الرقمية، وسنستعرض بعضها هنا:
- طريقة الفرق الأمامي
- طريقة الفرق الخلفي
- طريقة الفرق المركزي
كل طريقة لها مزاياها وعيوبها، وسنناقش كل منها بالتفصيل.
طريقة الفرق الأمامي
طريقة الفرق الأمامي تستخدم النقطة الحالية والنقطة التالية لحساب المشتقة. الصيغة هي: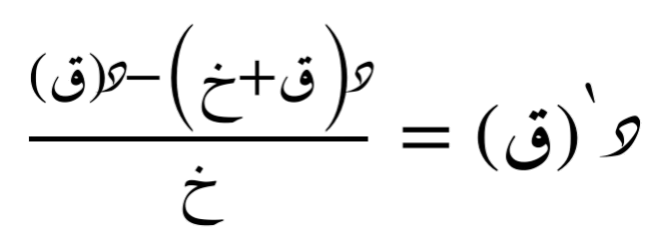
طريقة الفرق الخلفي
طريقة الفرق الخلفي تستخدم النقطة الحالية والنقطة السابقة لحساب المشتقة. الصيغة هي: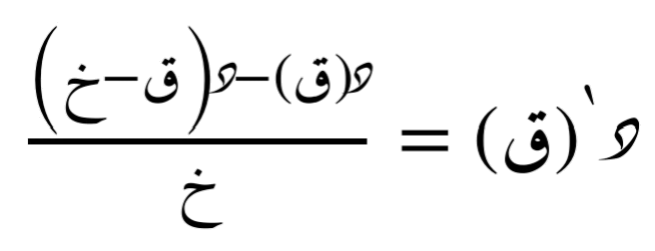
طريقة الفرق المركزي
طريقة الفرق المركزي تستخدم النقطة السابقة والنقطة التالية لحساب المشتقة. هذه الطريقة تعطي تقديرًا أكثر دقة للمشتقة. الصيغة هي:
حيث خ هو الفارق بين النقاط.
المتسلسلة الحدودية التفاضلية
نحصل على هذه العِبارات عن طريق المتسلسلة الحدودية التفاضلية التي تُقرّب أي دالّة د(س) حول النقطة ق.
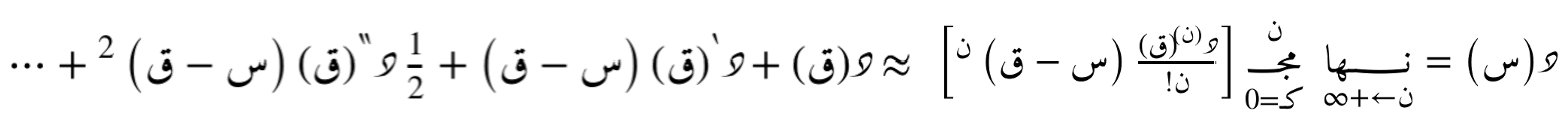
تُعرف هذه المتسلسلة أيضًا باسم متسلسلة تايلور، وقد سُمّيت بذلك نسبةً إلى عالم الرياضيات البريطاني بروك تايلور الذي قدّمها في القرن الثامن عشر لتقريب الدوال حول نقطة معيّنة.
أدلّة نظرية للتقريب الدالّة حسب درجة المتسلسلة
الدرجة المنعدمة
الدرجة المنعدمة من المتسلسلة الحدودية التفاضلية تعني أننا نستخدم قيمة الدالة عند النقطة فقط، دون استخدام مشتقاتها. الصيغة هي: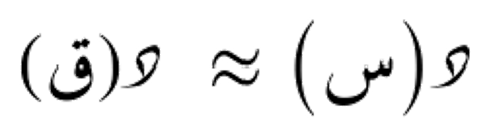
الدرجة الأولى
الدرجة الأولى من المتسلسلة الحدودية التفاضلية تعني أننا نستخدم قيمة الدالة ومشتقتها الأولى عند النقطة.
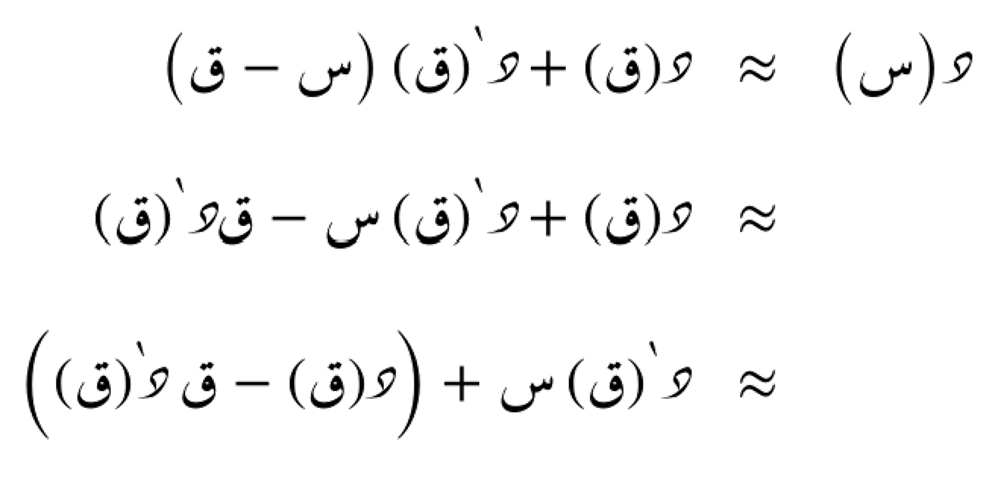
الدرجة الثانية
الدرجة الثانية من المتسلسلة الحدودية التفاضلية تعني أننا نستخدم قيمة الدالة ومشتقتها الأولى والثانية عند النقطة.
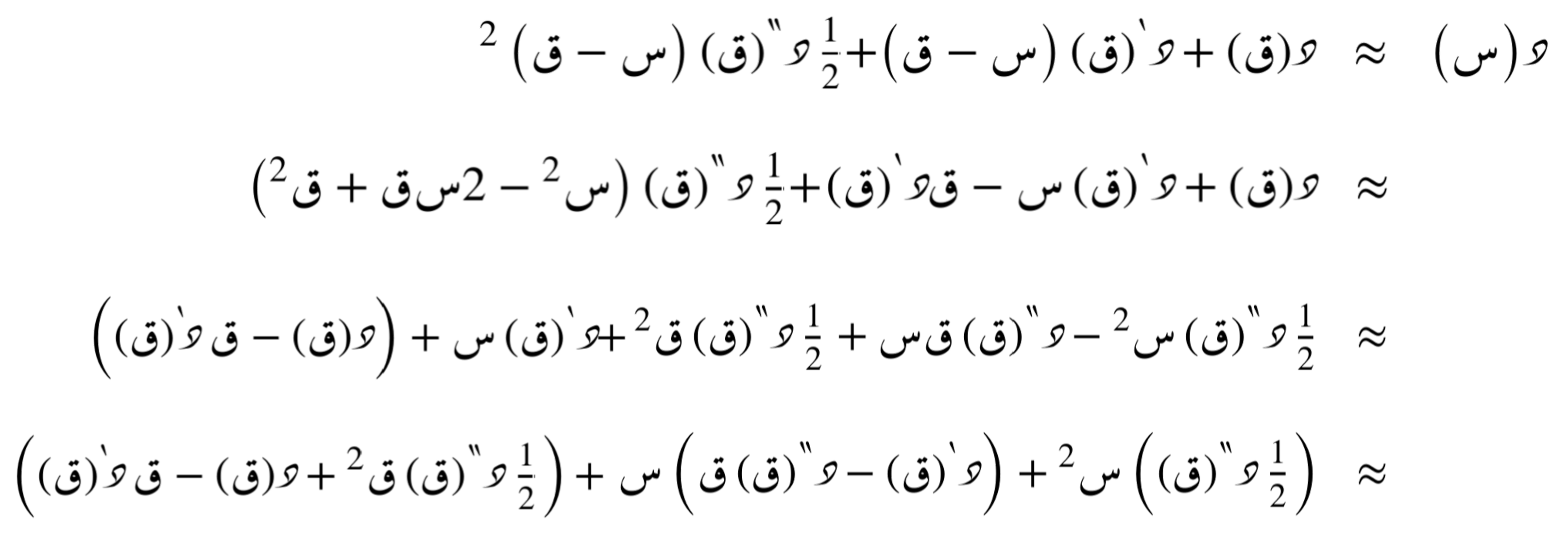
الدرجة الثالثة
الدرجة الثالثة من المتسلسلة الحدودية التفاضلية تعني أننا نستخدم قيمة الدالة ومشتقتها الأولى والثانية والثالثة عند النقطة.
خلاصة
تُعدّ المتسلسلة الحدودية التفاضلية أداة رياضية أساسية لتقريب الدوال حول نقطة معيّنة، حيث تزداد دقّة التقريب بازدياد درجة المتسلسلة، وإن كان ذلك يتطلّب حساب مشتقات أعلى للدالة. وتكمن أهمية هذه المتسلسلة في تطبيقاتها الواسعة في مجالات تحليل البيانات، والنمذجة الرياضية، والفيزياء، إذ تتيح تقريب الدوال وحساب مشتقاتها عددياً بكفاءة وموثوقية، مما يجعلها من الركائز النظرية والعملية في التحليل الرياضي.
المشتقات الرقمية باستخدام المتسلسلة الحدودية التفاضلية
تُسمّى العبارة أعلاه الصيغة التوسّعية للمتسلسلة ويُمكن إعادة كتابتها حسب الصيغة التضايفية.
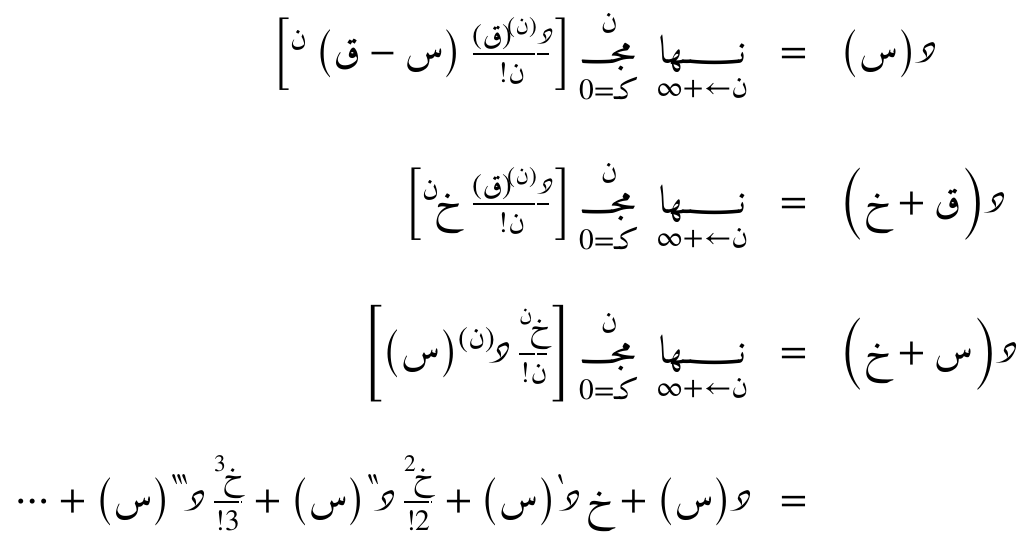
تُوفّر هذه الصيغة التضايفية للمتسلسلة الحدودية التفاضلية أساسًا رياضيًا دقيقًا لتقريب المشتقات عند نقطة معيّنة بالاعتماد على قيم الدالة في نقاط مجاورة. وتُعدّ هذه المتسلسلة أداة مركزية في التحليل العددي، إذ تتيح اشتقاق صيغ تقريبية للمشتقات من مختلف الرتب، وتُستخدم على نطاق واسع في التطبيقات العلمية والهندسية التي تتطلّب حساب المشتقات عددياً عند نقاط متفرقة أو عندما يتعذّر الحصول على تعبير تحليلي صريح للدالة.
أدلّة نظرية للتقريب المُشتقات حسب درجة المتسلسلة
تقريب من الدرجة الأولى للمُشتقة الأولى
التقريب من الدرجة الأولى للمُشتقة الأولى هي فقط تسمية أخرى لصيغة الفروق الأمامية.
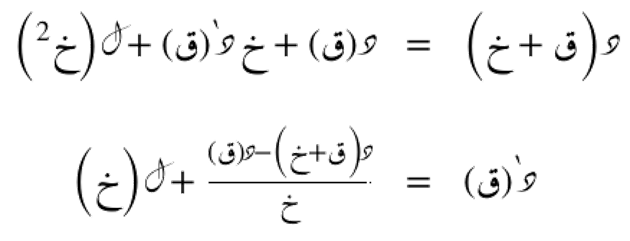
مع ل(خ) دالة الخطأ بدلالة الخُطوة خ.
ل(خ) هو مقدار الخطأ الناتج عن تقريب المشتقة باستخدام صيغة الفروق الأمامية. هذا الخطأ يُسمّى "خطأ القطع"، ويعتمد على حجم الخطوة خ وعلى مدى تغيّر الدالة. كلما صغرت قيمة خ، قلّ الخطأ، لكن لا يختفي تمامًا إلا إذا كانت خ تساوي صفرًا (وهو غير ممكن عمليًا). عادةً يكون ل(خ) متناسبًا مع خ نفسه في هذا التقريب، أي أن الخطأ يقل خطيًا مع تصغير خ.
تقريب من الدرجة الثانية للمُشتقة الأولى
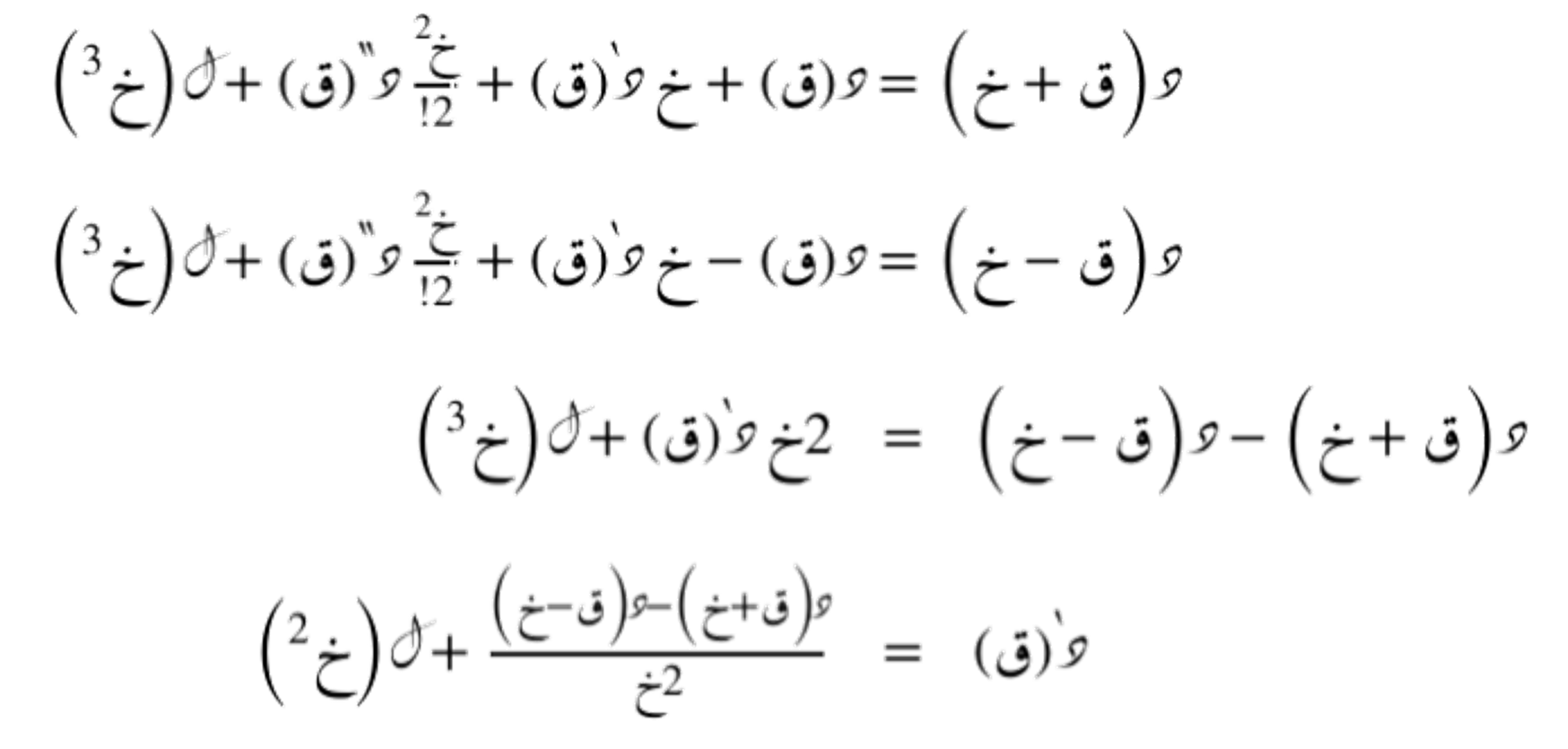
تقريب من الدرجة الثانية للمُشتقة الثانية
التقريب من الدرجة الثانية للمُشتقة الثانية يُعرف بصيغة الفروق المركزية، ويُستخدم للحصول على تقدير أدق للمُشتقة الثانية عند نقطة معيّنة بالاعتماد على قيم الدالة في النقاط المجاورة. تعتمد هذه الصيغة على إلغاء الحدود من الدرجة الثانية في متسلسلة تايلور، مما يقلل من مقدار الخطأ ويزيد من دقّة التقريب مقارنةً بالطرق الأبسط.
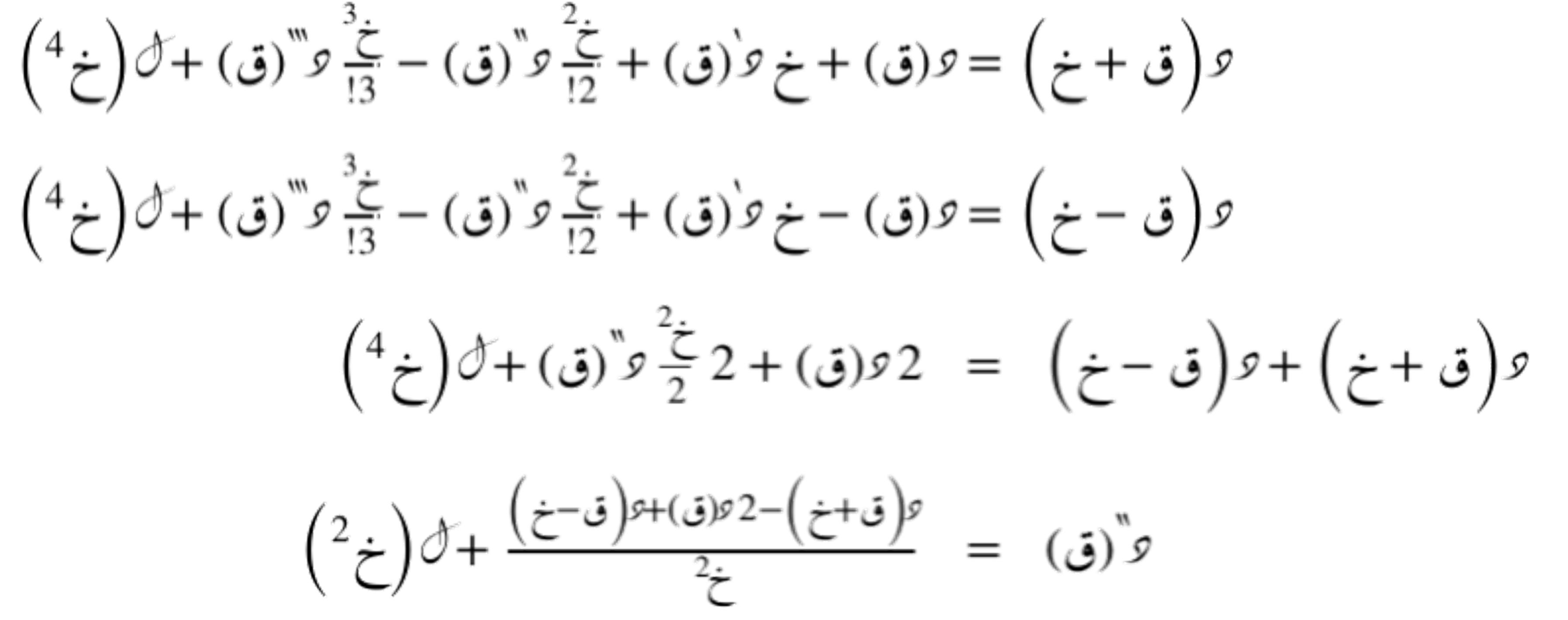
تقريب من الدرجة الرابعة للمُشتقة الثانية
يُمثّل هذا التقريب صيغة متقدّمة للفروق المركزية للمُشتقة الثانية، حيث يأخذ في الاعتبار حدود المتسلسلة حتى الدرجة الرابعة، ويعتمد على قيم الدالة في نقاط متعددة حول النقطة المدروسة، وليس فقط على النقاط السابقة أو اللاحقة مباشرةً. يتيح هذا الأسلوب تحسين دقّة التقريب بشكل ملحوظ مقارنةً بالطرق الأبسط، ويُستخدم في التطبيقات التي تتطلّب تقديراً عددياً عالي الدقّة للمُشتقات.
فيما يلي صيغة المتسلسلة الحدودية التفاضلية مع توسّع أكبر للخطوة، حيث تشمل حدودًا أعلى مثل خُطوتين أو ثلاث أو أربع، مما يسمح بالحصول على تقريبات عددية أكثر دقة للمشتقات من رتب أعلى. هذا التوسّع يُستخدم في التحليل العددي لتقليل مقدار الخطأ وزيادة موثوقية النتائج، خاصة عند التعامل مع دوال ذات تغيّر سريع أو عند الحاجة إلى تقديرات دقيقة للمشتقات في التطبيقات العلمية والهندسية.
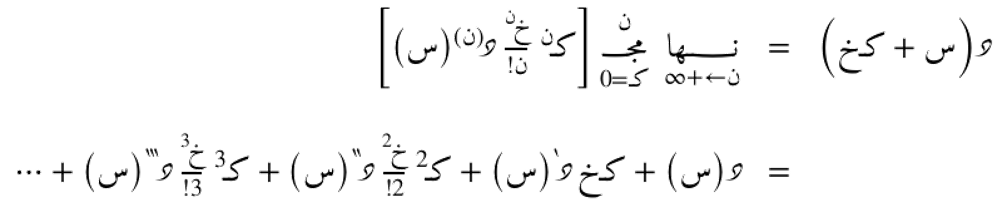
فيما يلي نتتبع خُطوات إيجاد الصيغة من خلال أولّاً:
حساب الدالة عند النقاط المُعتَبرة
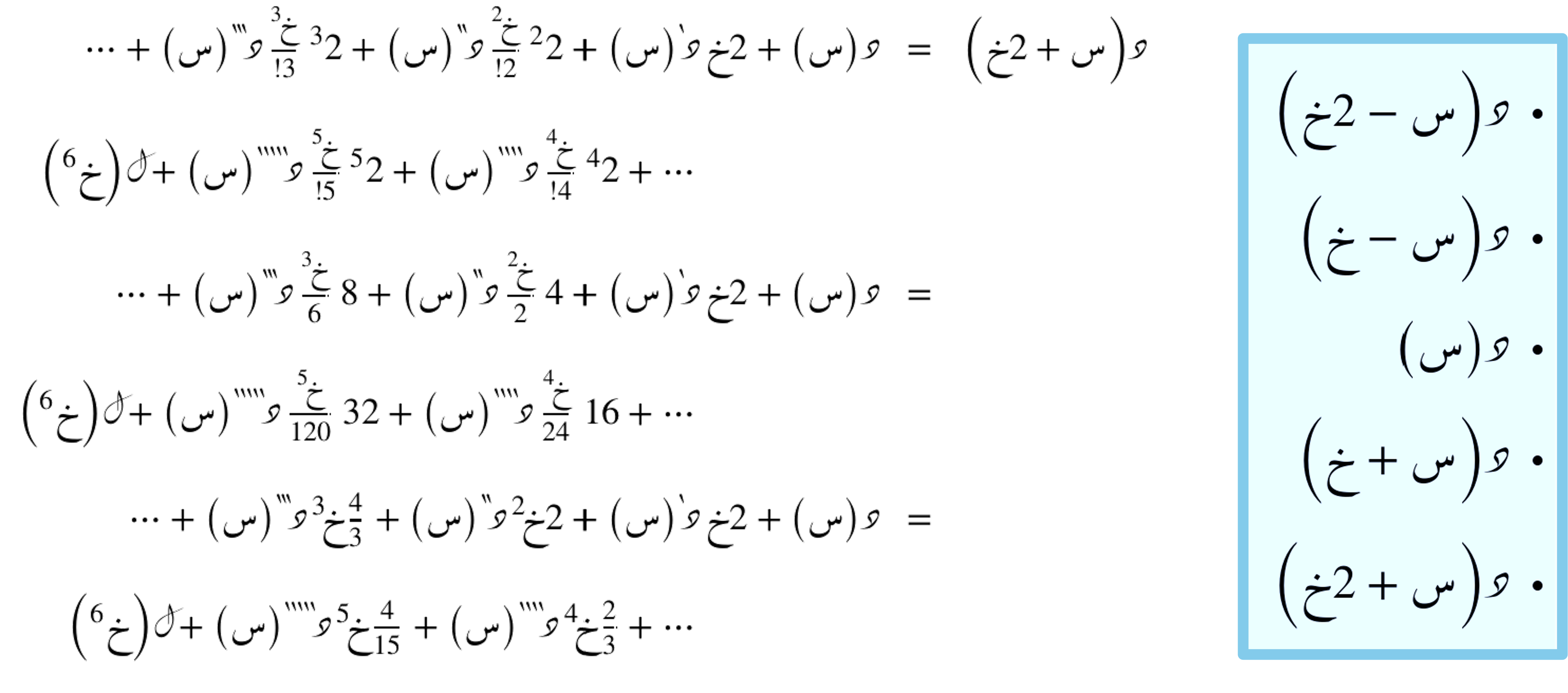
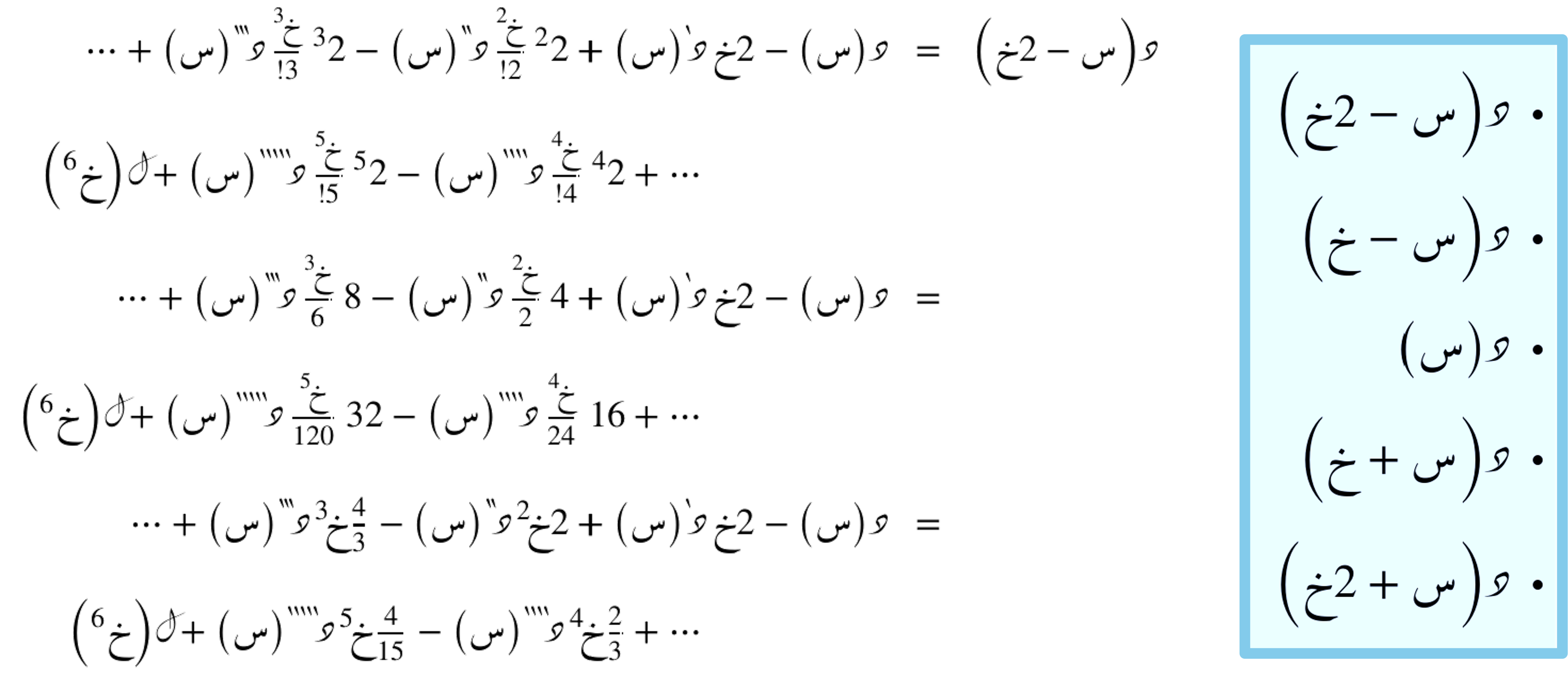
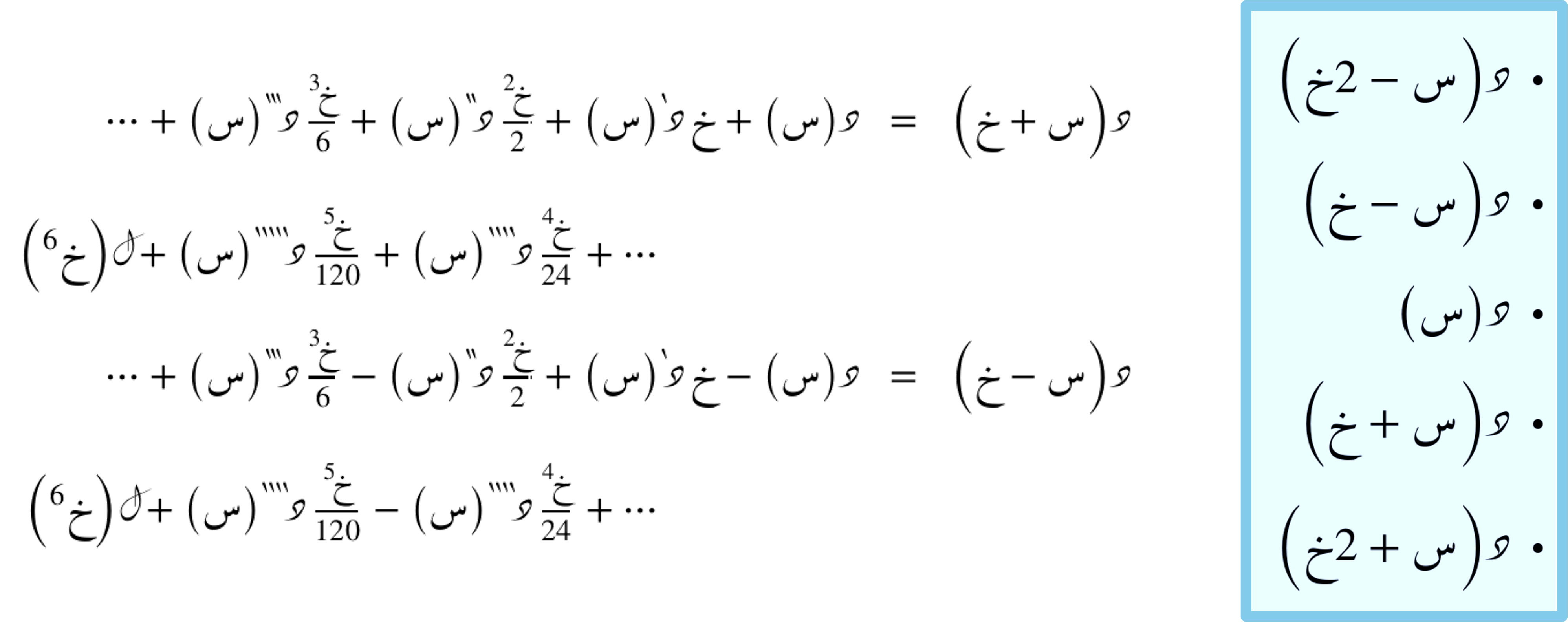
بِناء نِظمة المعادلات
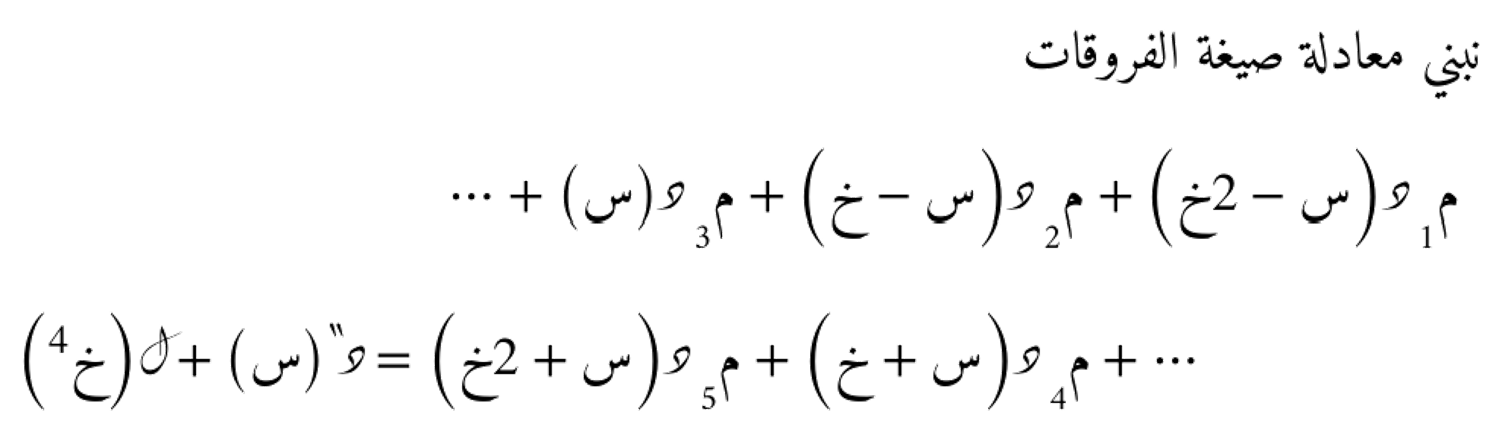
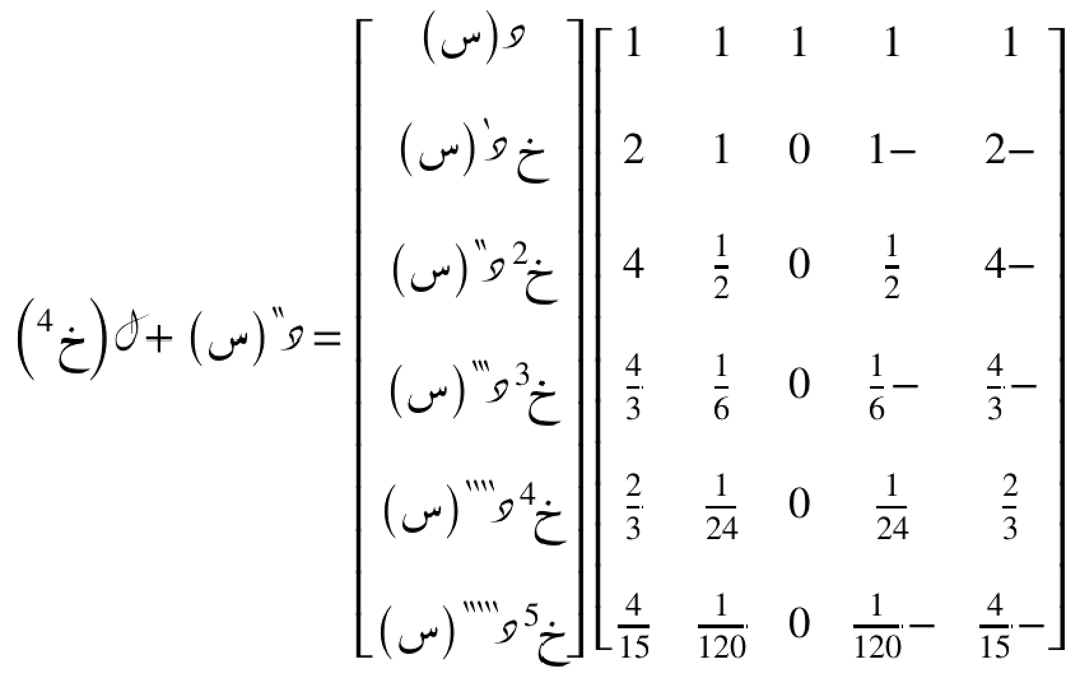
جبر المعاملات المضروبة في كلّ حد
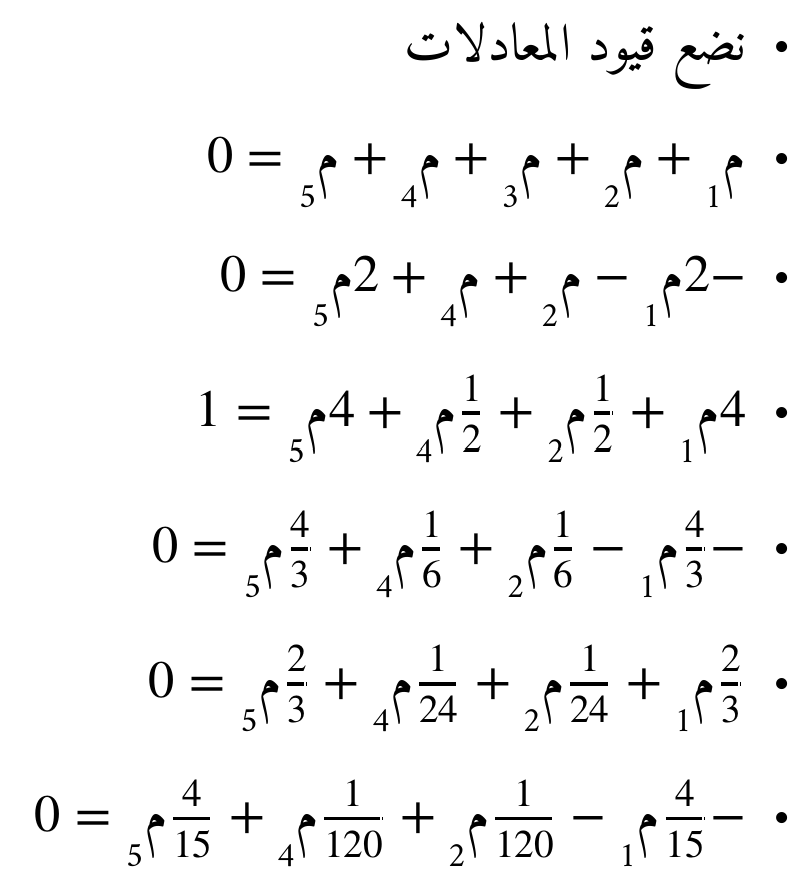

و منه يمكننا الإستنتاج أن: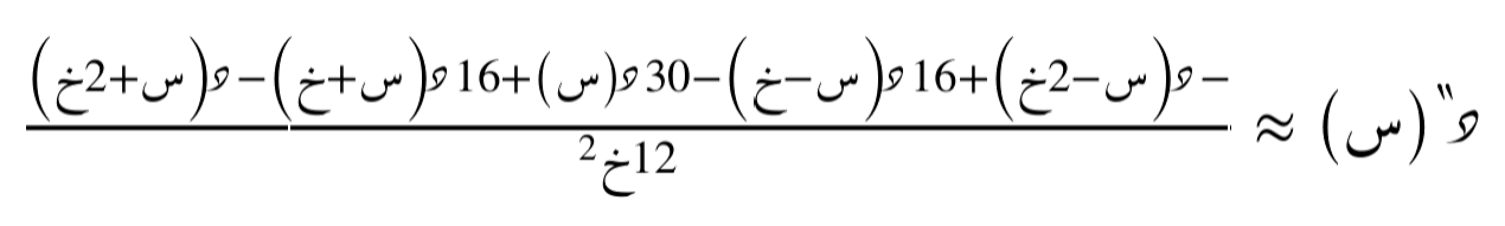
جدول مُعاملات صيَغ الفروق المركزية لتقريب المشتقات
فيما يلي جدول يوضح معاملات صيَغ الفروق المركزية لتقريب المشتقات من الدرجات المختلفة والتي يُمكن حسابتها بنفس المنهج أعلاه:
| الخطوة | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| المُشتقة | الدرجة | -٥ | -٤ | -٣ | -٢ | -١ | ٠ | ١ | ٢ | ٣ | ٤ | ٥ |
| ١ | ٢ | -1\2 | 0 | 1\2 | ||||||||
| ٤ | -1\12 | 2\3 | 0 | -2\3 | 1\12 | |||||||
| ٦ | -1\60 | 3\20 | -3\4 | 0 | 3\4 | -3\20 | 1\60 | |||||
| ٨ | 1\280 | -4\105 | 1\5 | -4\5 | 0 | 4\5 | -1\5 | 4\105 | -1\280 | |||
| ٢ | ٢ | 1 | -2 | 1 | ||||||||
| ٤ | -1\12 | 4\3 | -5\2 | 4\3 | -1\12 | |||||||
| ٦ | 1\90 | -3\20 | 3\2 | -49\18 | 3\2 | -3\20 | 1\90 | |||||
| ٨ | -1\560 | 8\315 | 1\5 | 8\5 | -205\72 | 8\5 | 1\5 | 8\315 | -1\560 | |||
| ٣ | ٢ | -1\2 | 1 | 0 | -1 | 1\2 | ||||||
| ٤ | 1\8 | -1 | 13\8 | 0 | -13\8 | 1 | -1\8 | |||||
| ٦ | -7\240 | 3\10 | -169\120 | 61\30 | 0 | -61\30 | 169\120 | -3\10 | 7\240 | |||
| ٤ | ٢ | 1 | -4 | 6 | -4 | 1 | ||||||
| ٤ | -1\6 | 2 | -13\2 | 28\3 | -13\2 | 2 | -1\6 | |||||
| ٦ | 7\240 | -2\5 | 169\60 | -122\15 | 91\8 | -122\15 | 169\60 | -2\5 | 7\240 | |||
هذا الجدول يُظهر معاملات الفروق المركزية للمشتقات من الدرجات المختلفة، حيث يُمكن استخدامه لتقريب المشتقات عند نقاط مختلفة باستخدام قيم الدالة في تلك النقاط. كلما زادت درجة التقريب، زادت دقّة النتيجة، ولكن أيضًا زادت تعقيد الحسابات.
تحليل الخطأ
خطأ التقريب: ماذا يعني أن يكون التقريب من درجة ما ؟
عند استخدام طرق الإشتقاق الرقمي، يكون هناك دائمًا خطأ في التقريب. هذا الخطأ يعتمد على حجم الخطوة خ وعلى طبيعة الدالة نفسها. كلما كانت خ أصغر، كان التقريب أفضل، ولكن إذا كانت خ كبيرة جدًا، فإن الخطأ يزداد.
يُمكن تحليل الخطأ الناتج عن التقريب باستخدام المتسلسلة الحدودية التفاضلية. إذا كانت الدالة د(س) قابلة للاشتقاق حتى الرتبة ن، فإن الخطأ في التقريب من الدرجة ن يكون متناسبًا مع خ(ن+1). هذا يعني أن الخطأ يتناقص بشكل أسرع كلما زادت درجة التقريب.
على سبيل المثال، إذا كان لدينا تقريب من الدرجة الأولى، فإن الخطأ سيكون متناسبًا مع خ2. إذا كان لدينا تقريب من الدرجة الثانية، فإن الخطأ سيكون متناسبًا مع خ3، وهكذا.
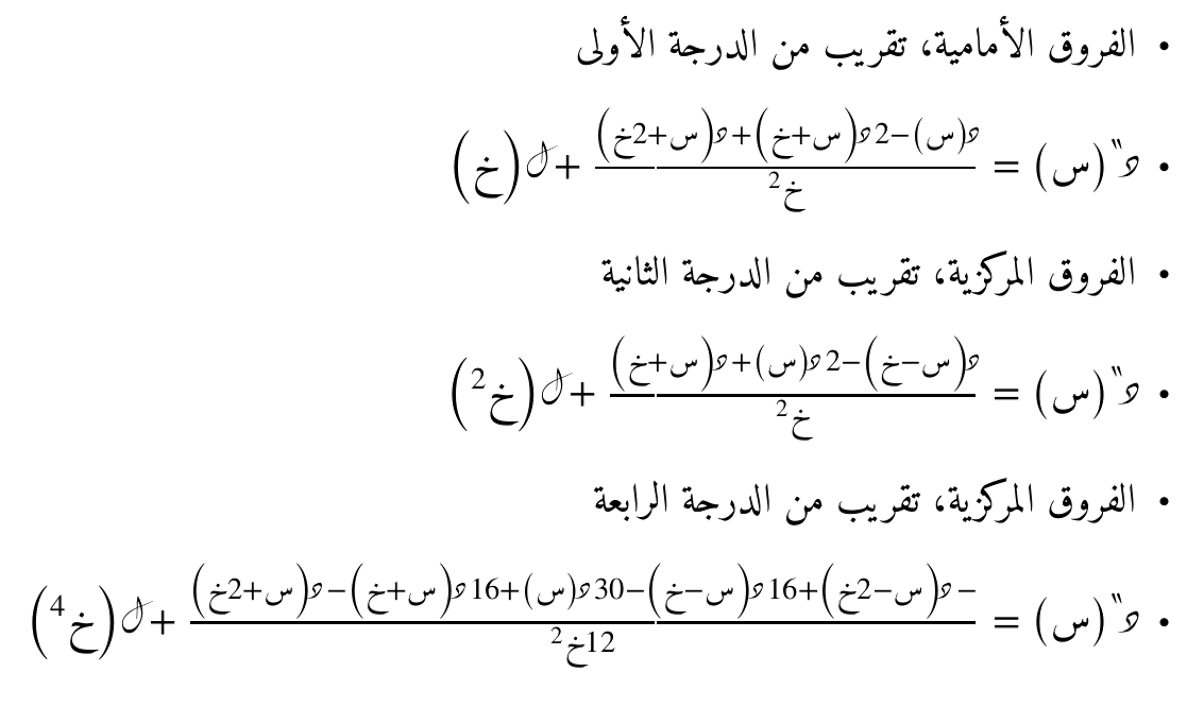
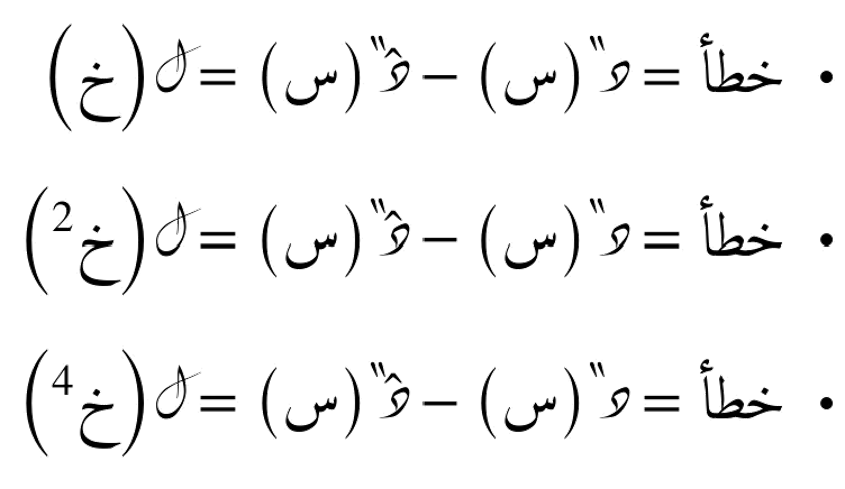
في الرسمين البيانيين أدناه، نلاحظ كيف يتغير مقدار الخطأ في تقريب المشتقة مع تغيّر قيمة الخطوة خ ولدرجات تقريب مختلفة (الأولى، الثانية، والرابعة). يوضّح الرسم الأول العلاقة على مقياس عادي، بينما يُظهر الرسم الثاني العلاقة على مقياس لوغاريتمي مزدوج.
كلما ارتفعت درجة التقريب (أي استخدمنا صيغة من رتبة أعلى)، أصبح الخطأ أصغر بكثير لنفس قيمة خ. كما نلاحظ أن الخطأ يتناقص بسرعة أكبر مع تصغير خ عند استخدام تقريبات من درجات أعلى. هذا يؤكد أهمية اختيار صيغة تقريب مناسبة للحصول على نتائج دقيقة، خاصة عند الحاجة إلى تقليل الخطأ العددي.
عند استخدام مقياس لوغاريتمي مزدوج (لو-لو)، تظهر العلاقات التي تتبع قوانين أسية أو حدودية (مثل الخطأ مقابل الخطوة خ في تقريبات المشتقات) كخطوط مستقيمة تقريبًا. هذا لأن كثيرات الحدود أو العلاقات التناسبية من الشكل تتحول إلى علاقة خطية عند أخذ اللوغاريتم للطرفين. لذلك، إذا كان الخطأ يتناسب مع قوة للخطوة، فإن الرسم البياني على مقياس لوغاريتمي مزدوج يُظهر ميل الخط المستقيم مساوٍ لدرجة القوة، مما يسهل تحليل سلوك الخطأ وتحديد رتبة التقريب بصريًا.
تتحول إلى علاقة خطية عند أخذ اللوغاريتم للطرفين. لذلك، إذا كان الخطأ يتناسب مع قوة للخطوة، فإن الرسم البياني على مقياس لوغاريتمي مزدوج يُظهر ميل الخط المستقيم مساوٍ لدرجة القوة، مما يسهل تحليل سلوك الخطأ وتحديد رتبة التقريب بصريًا.
في هذا النوع من الرسوم البيانية، كل وحدة على المحور تمثل زيادة بمقدار قوة واحدة (أس واحد) في المقياس، أي أن الانتقال من قيمة إلى أخرى يعني ضرب أو قسمة القيمة على 10 (أو على أساس اللوغاريتم المستخدم).
أهمية اختيار خطوة صغيرة (خ)
عند استخدام طرق الإشتقاق الرقمي، تلعب قيمة الخطوة خ دورًا أساسيًا في دقّة التقريب. كلما كانت خ أصغر، اقتربت النتيجة العددية للمشتقة من القيمة الحقيقية للمشتقة التحليلية. لكن إذا كانت خ كبيرة جدًا، يصبح التقريب خشنًا ويزداد الخطأ. بالمقابل، إذا كانت خ صغيرة جدًا، قد تظهر أخطاء عددية بسبب حدود دقة الحاسوب (خطأ التقريب العشري).
لذلك، يجب اختيار خ بحيث تكون صغيرة بما يكفي للحصول على تقريب جيد، ولكن ليست صغيرة جدًا لتجنّب الأخطاء العددية. غالبًا ما يتم تحديد قيمة خ بالتجربة أو حسب طبيعة الدالة والبيانات المتوفرة.













