الإشتقاق الرقمي
متعدد المتغيّرات
الإشتقاق الرقمي متعدد المتغيّرات
عندما تكون الدالة تعتمد على أكثر من متغيّر، فإن الاشتقاق الرقمي يصبح أكثر تعقيدًا ويتطلّب استخدام اشتقاقات جزئية بالنسبة إلى كل متغيّر. في هذا القسم نستعرض طرق تقريب المشتقات الجزئية باستخدام المتسلسلة الحدودية التفاضلية.
١. دالّة ذات متغيّر واحد
في هذا القسم، نستعرض طرق الاشتقاق الرقمي لدالة تعتمد على متغيّر واحد، باستخدام المتسلسلة الحدودية التفاضلية. هذه الطرق تشمل اشتقاقات من الدرجة المنعدمة إلى الدرجة العامة.
ملاحظة: هذا القسم هو للمراجعة فقط، حيث تم شرحه في الدروس السابقة. إذا كنت بحاجة إلى مراجعة، يمكنك الرجوع إلى الدرس السابق حول الاشتقاق الرقمي أحادي المتغيّر.
مُتغيّر واحد

الدرجة المنعدمة
الصيغة التوسّعية حول نُقطة ما
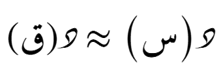
الصيغة التضايُفية حول أي نُقطة
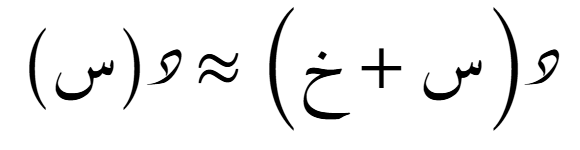
الدرجة الأولى
الصيغة التوسّعية حول نُقطة ما
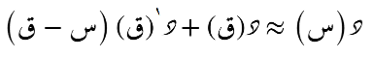
الصيغة التضايُفية حول أي نُقطة
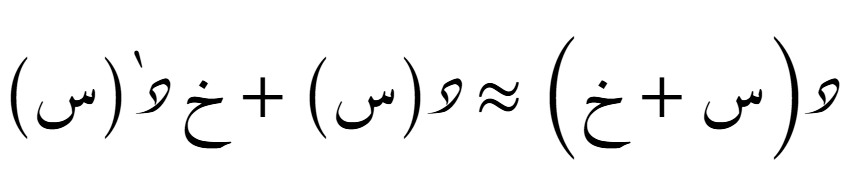
الدرجة الثانية
الصيغة التوسّعية حول نُقطة ما
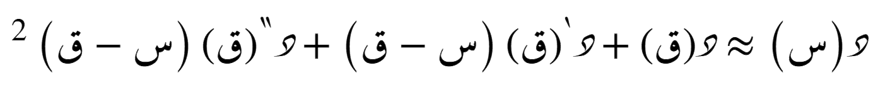
الصيغة التضايُفية حول أي نُقطة
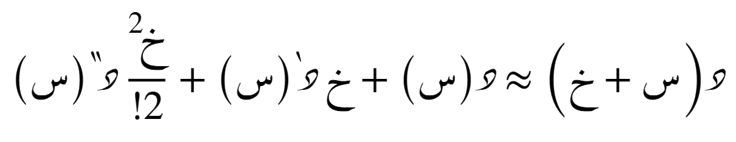
الدرجة الثالثة
الصيغة التوسّعية حول نُقطة ما
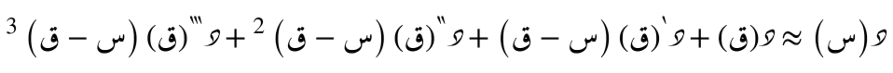
الصيغة التضايُفية حول أي نُقطة

الدرجة العامة
الصيغة التوسّعية حول نُقطة ما
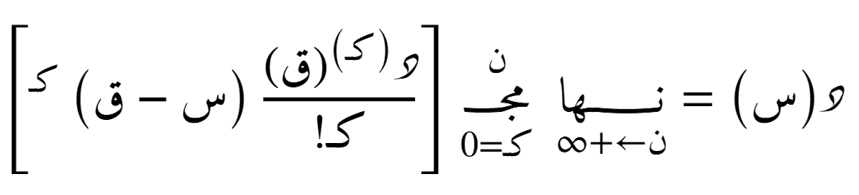
الصيغة التضايُفية حول أي نُقطة
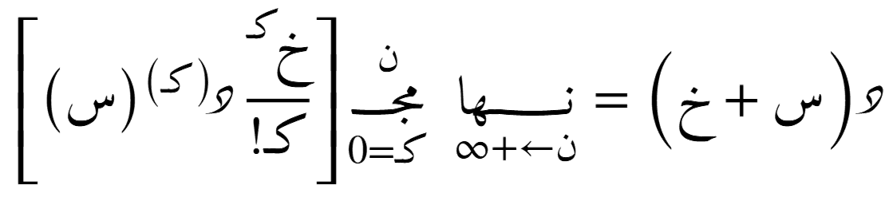
٢. دالّة ذات متغيّرين
عندما تكون الدالة تعتمد على متغيّرين، فإن الاشتقاق الرقمي يتطلّب استخدام اشتقاقات جزئية بالنسبة إلى كل متغيّر. في هذا القسم نستعرض طرق تقريب المشتقات الجزئية باستخدام المتسلسلة الحدودية التفاضلية.
الاشتقاق حسب المتغيّرين

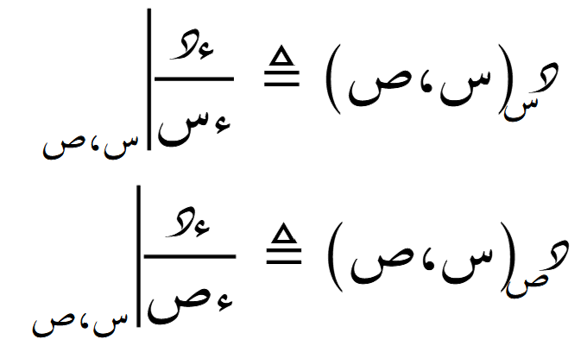
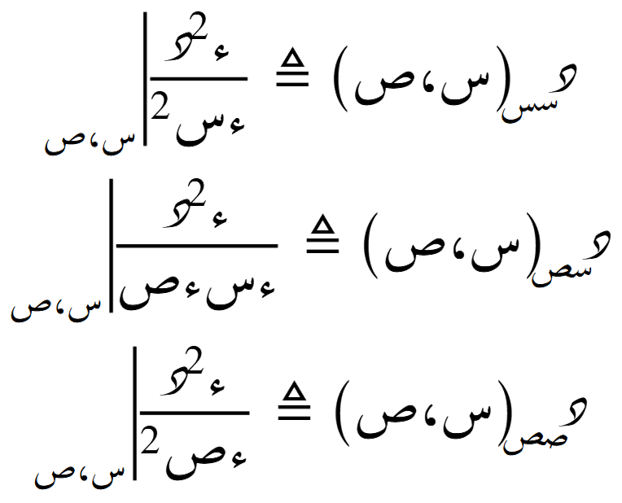
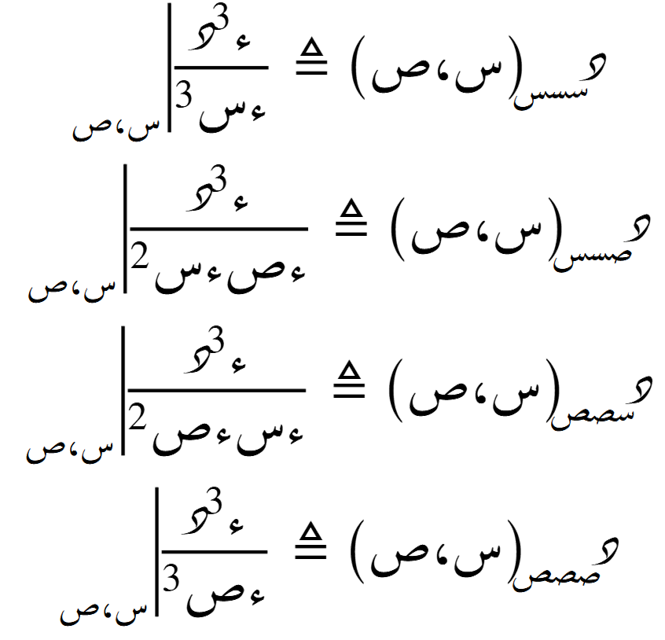
الدرجة المنعدمة
الصيغة التوسّعية حول نُقطة ما

الصيغة التضايُفية حول أي نُقطة
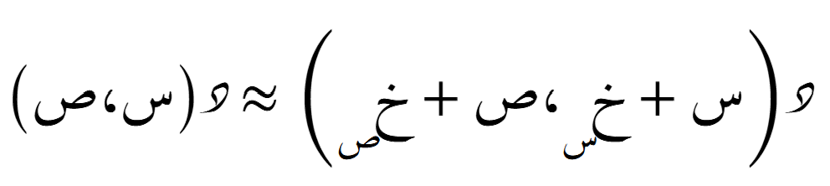
الدرجة الأولى
الصيغة التوسّعية حول نُقطة ما
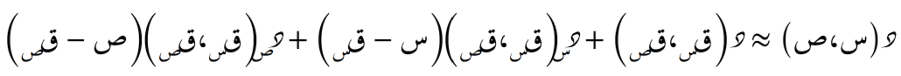
الصيغة التضايُفية حول أي نُقطة
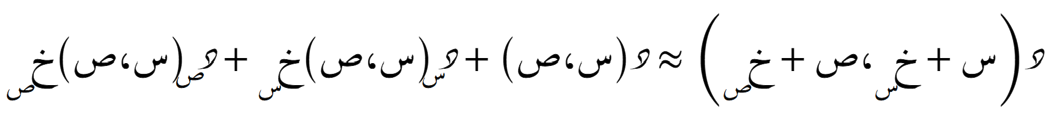
الدرجة الثانية
الصيغة التوسّعية حول نُقطة ما
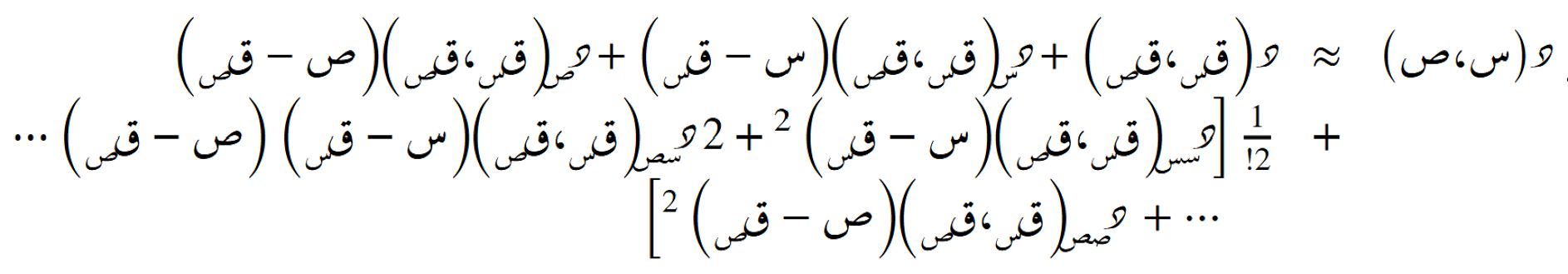
الصيغة التضايُفية حول أي نُقطة
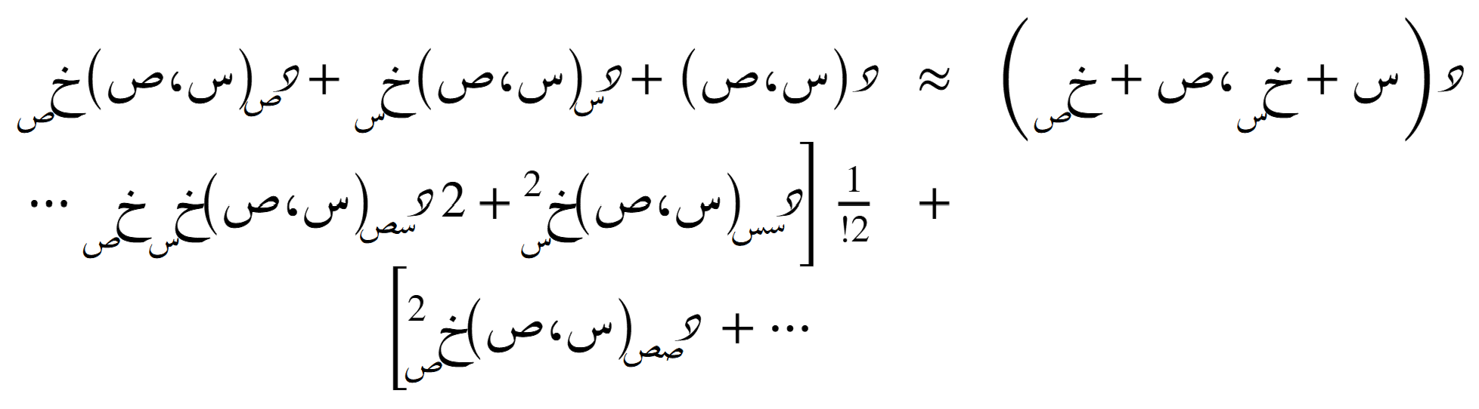
الدرجة الثالثة
الصيغة التوسّعية حول نُقطة ما
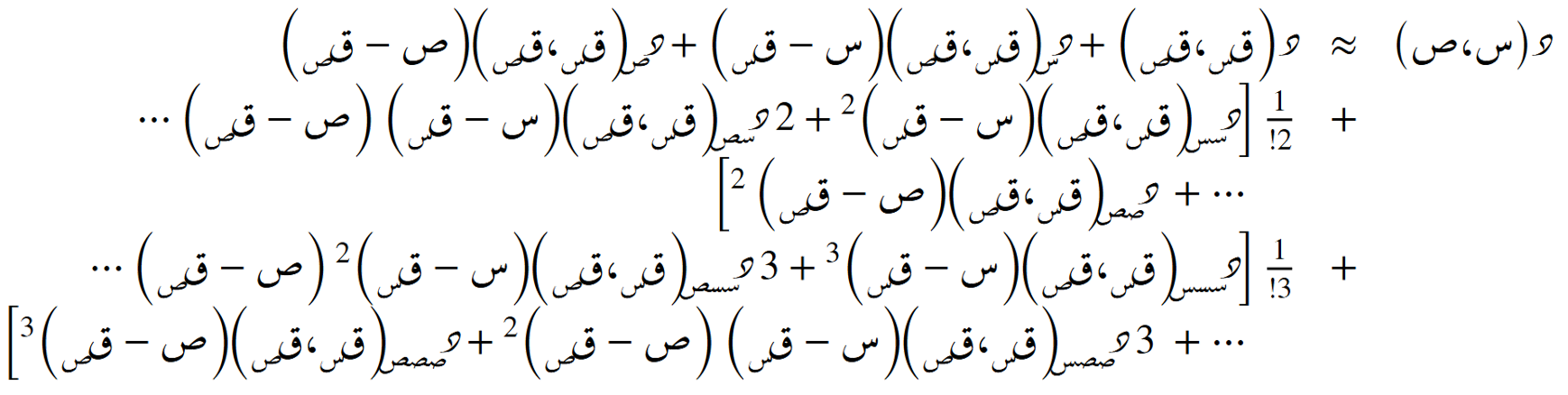
الصيغة التضايُفية حول أي نُقطة
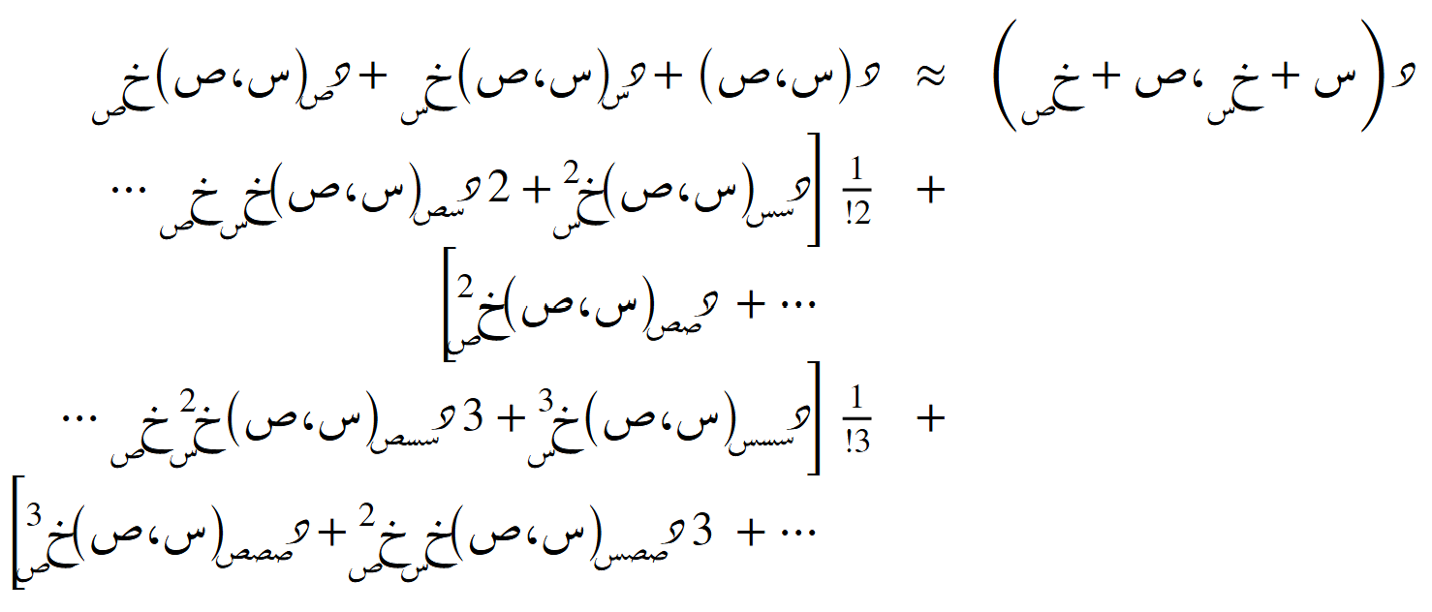
الدرجة العامة
الصيغة التوسّعية حول نُقطة ما
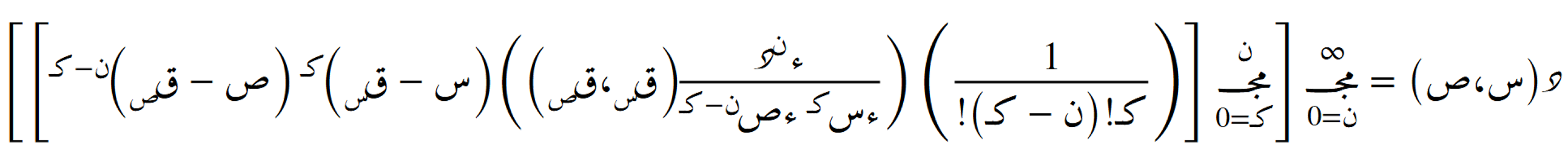
الصيغة التضايُفية حول أي نُقطة
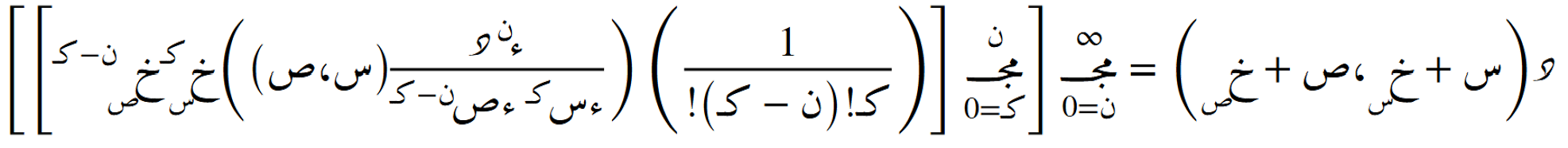
٣. دالّة ذات عدد عام من المتغيّرات (المُوترات)
المُتغيّرات
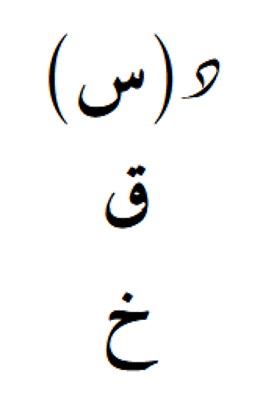
الدرجة المنعدمة
الصيغة التوسّعية حول نُقطة ما
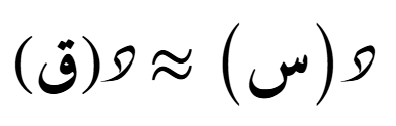
الصيغة التضايُفية حول أي نُقطة
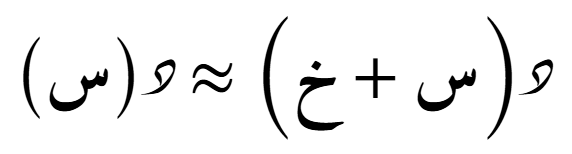
الدرجة الأولى
الصيغة التوسّعية حول نُقطة ما
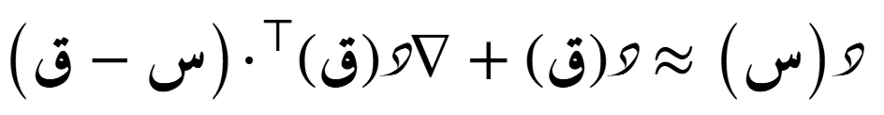
الصيغة التضايُفية حول أي نُقطة
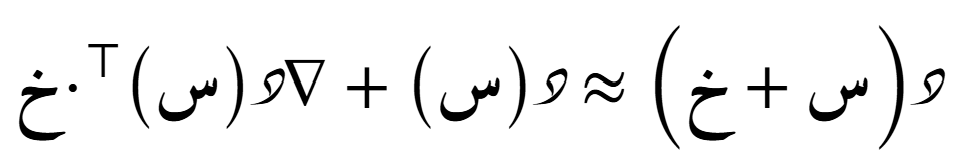
الدرجة الثانية
الصيغة التوسّعية حول نُقطة ما
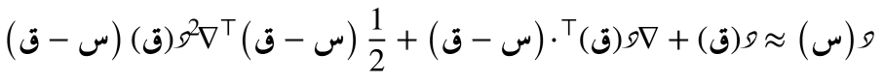
الصيغة التضايُفية حول أي نُقطة
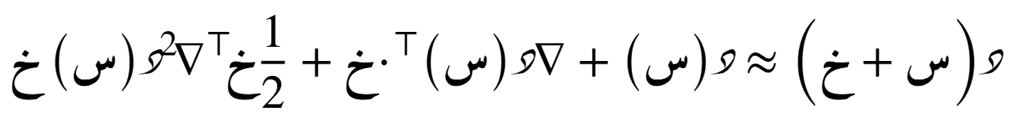
الدرجة الثالثة
الصيغة التوسّعية حول نُقطة ما
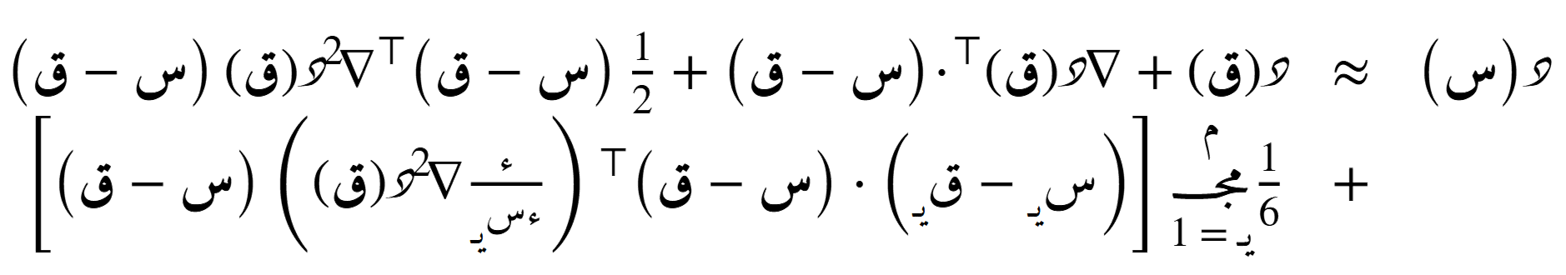
الصيغة التضايُفية حول أي نُقطة
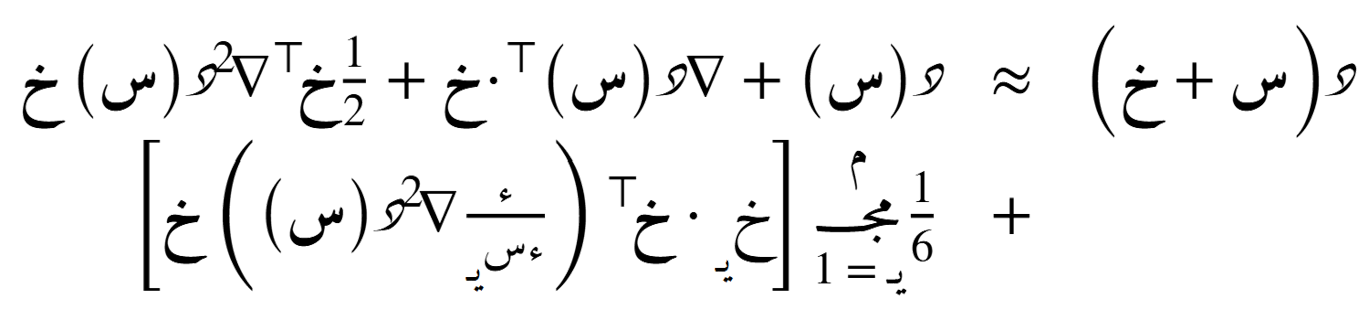
الدرجة الرابعة
الصيغة التوسّعية حول نُقطة ما
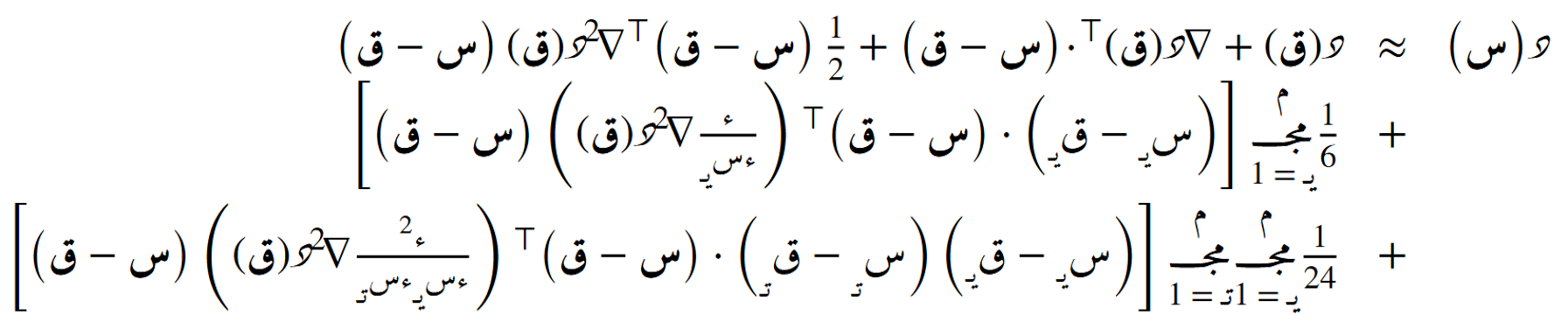
الصيغة التضايُفية حول أي نُقطة
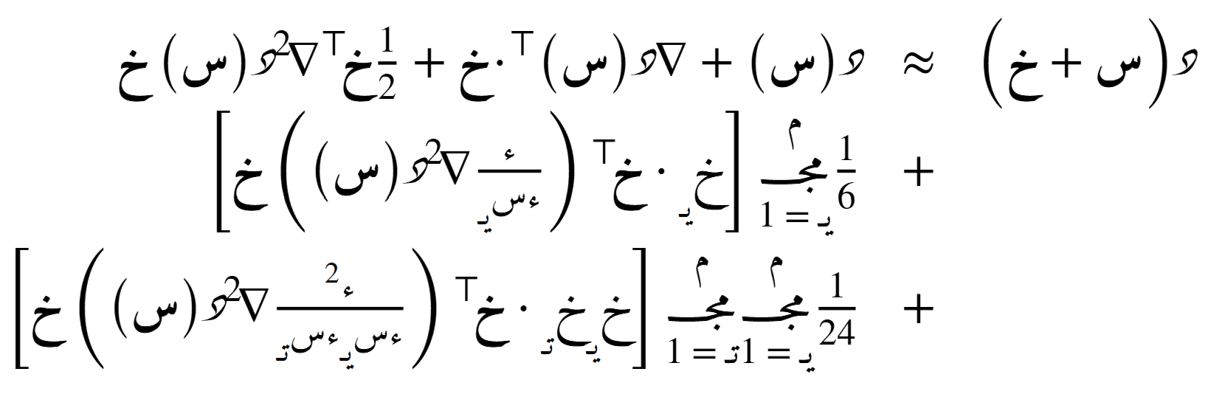
مصفوفة المشتقات: التنسورات
في حالة الدوال التي تعتمد على عدد عام من المتغيّرات، يمكننا استخدام المصفوفات لتمثيل المشتقات الجزئية. هذه المصفوفات تُعرف بالتنسورات، وهي تعطي معلومات حول كيفية تغير الدالة بالنسبة لكل متغيّر.
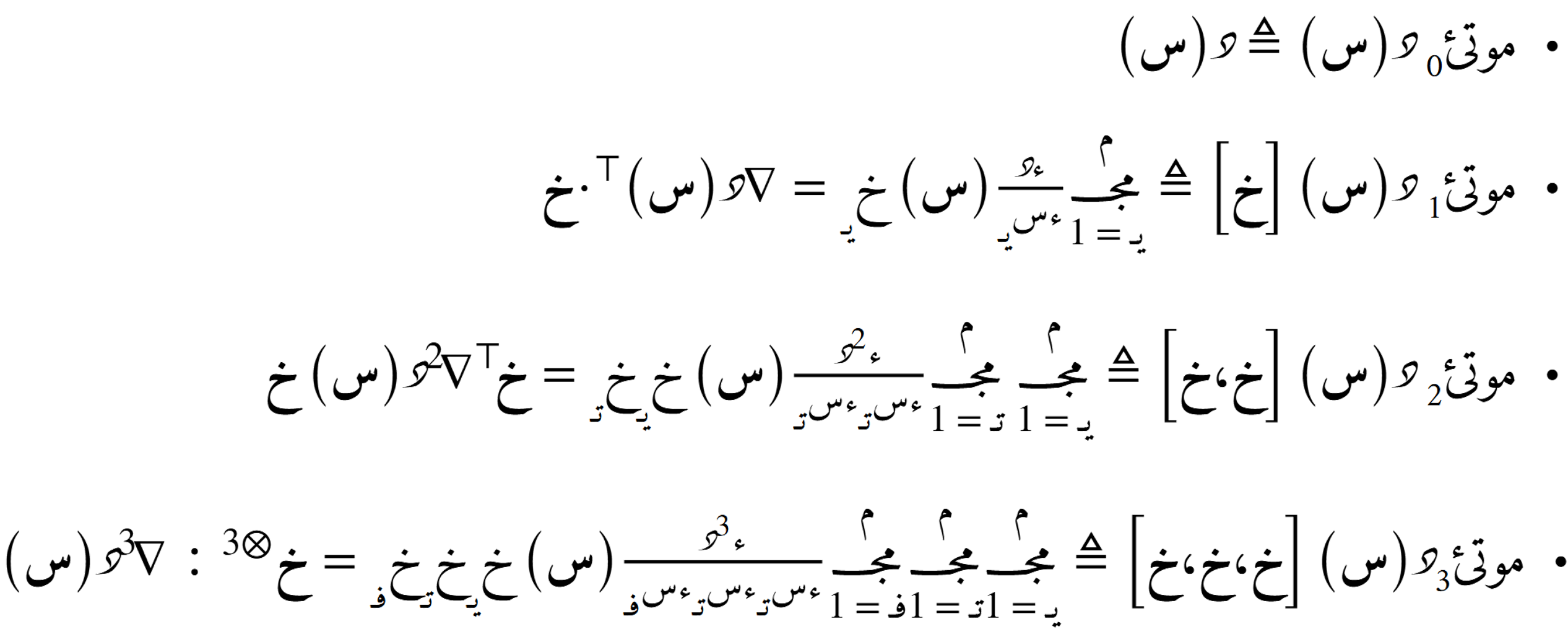
الدرجة العامة
الصيغة التوسّعية حول نُقطة ما
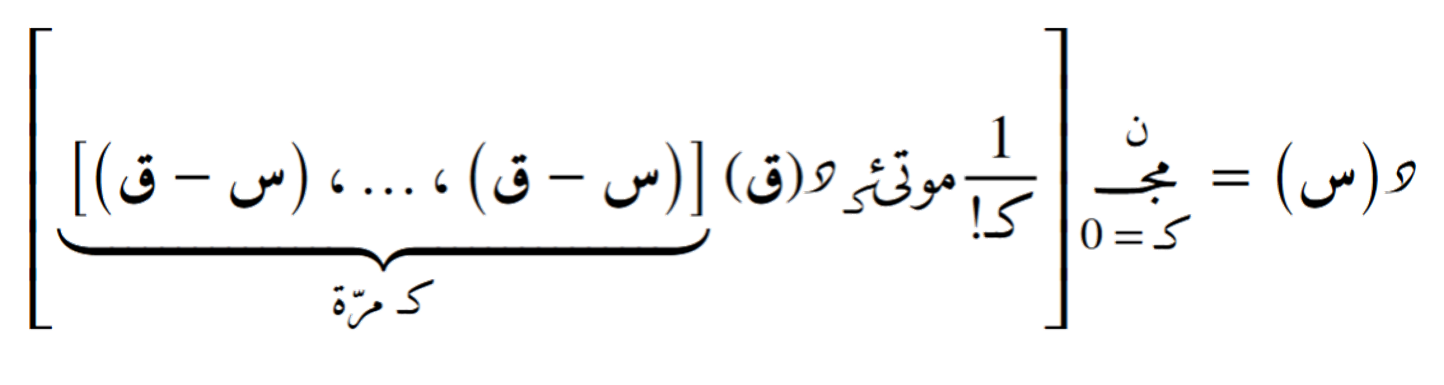
الصيغة التضايُفية حول أي نُقطة