التكامل الرقمي
أحادي المتغيّر
التكامل الرقمي
التكامل الرقمي هو طريقة لحساب التكاملات عندما لا يكون من الممكن حسابها تحليليًا أو عندما تكون القيم متاحة فقط كنقاط منفصلة. من أشهر هذه الطرق هي طريقة المستطيل.
في هذا القسم، سنشرح ثلاث طرق رئيسية لحساب التكامل الرقمي باستخدام المستطيلات: الطريقة الأمامية، الطريقة الخلفية، والطريقة المركزية.
طرق التكامل الرقمي بالمستطيلات
تشمل الطرق الأساسية:
- طريقة المستطيل الأمامي
- طريقة المستطيل الخلفي
- طريقة المستطيل المركزي
تختلف هذه الطرق في اختيار نقطة العينة داخل كل فترة، مما يؤثر على دقة النتيجة.

طريقة المستطيل الأمامي
في هذه الطريقة، يتم استخدام طرف الفترة الأيسر لحساب قيمة الدالة. الصيغة هي:
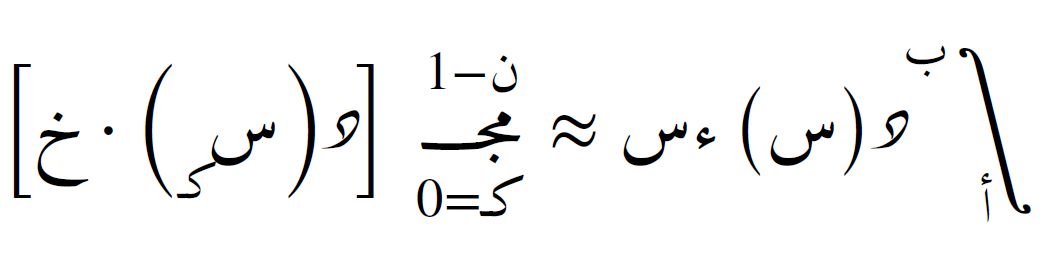
تميل هذه الطريقة إلى التقليل من التكامل إذا كانت الدالة تزداد.
طريقة المستطيل الخلفي
تستخدم هذه الطريقة الطرف الأيمن من كل فترة فرعية لحساب التكامل. الصيغة هي:
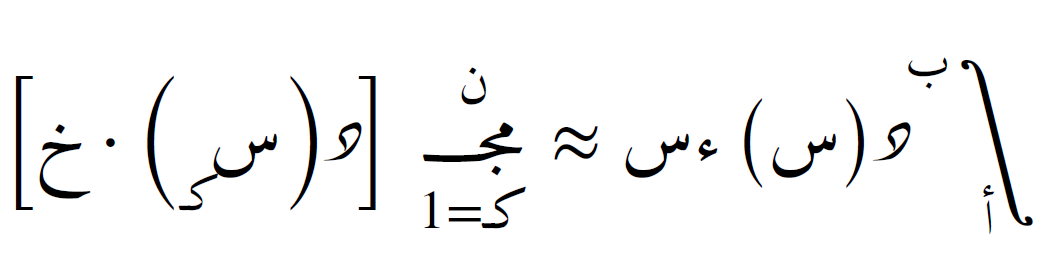
تميل إلى المبالغة في تقدير التكامل إذا كانت الدالة تزداد.
طريقة المستطيل المركزي
في هذه الطريقة، يتم استخدام نقطة المنتصف من كل فترة. وهي أكثر دقة من الطريقتين السابقتين. الصيغة هي:
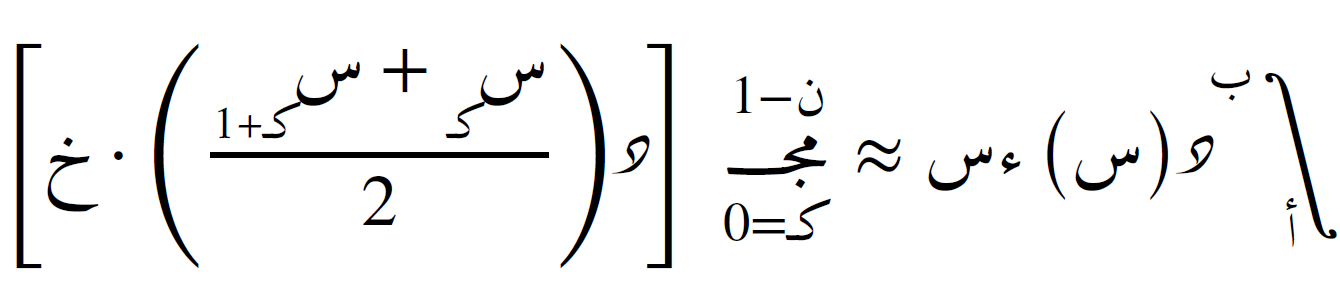
تمتاز هذه الطريقة بأنها أكثر دقة، وخطأها من الرتبة الثانية ل(خ2).
حيث خ هو طول الفترة الفرعية
و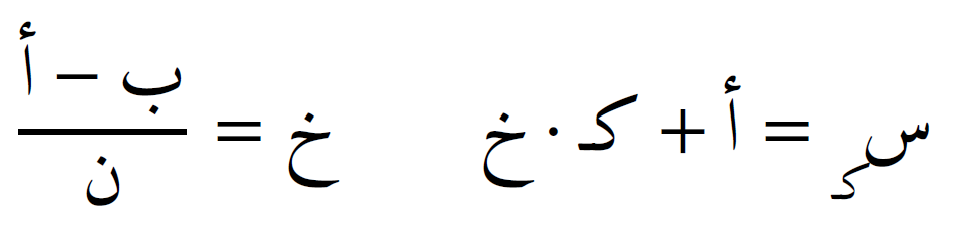
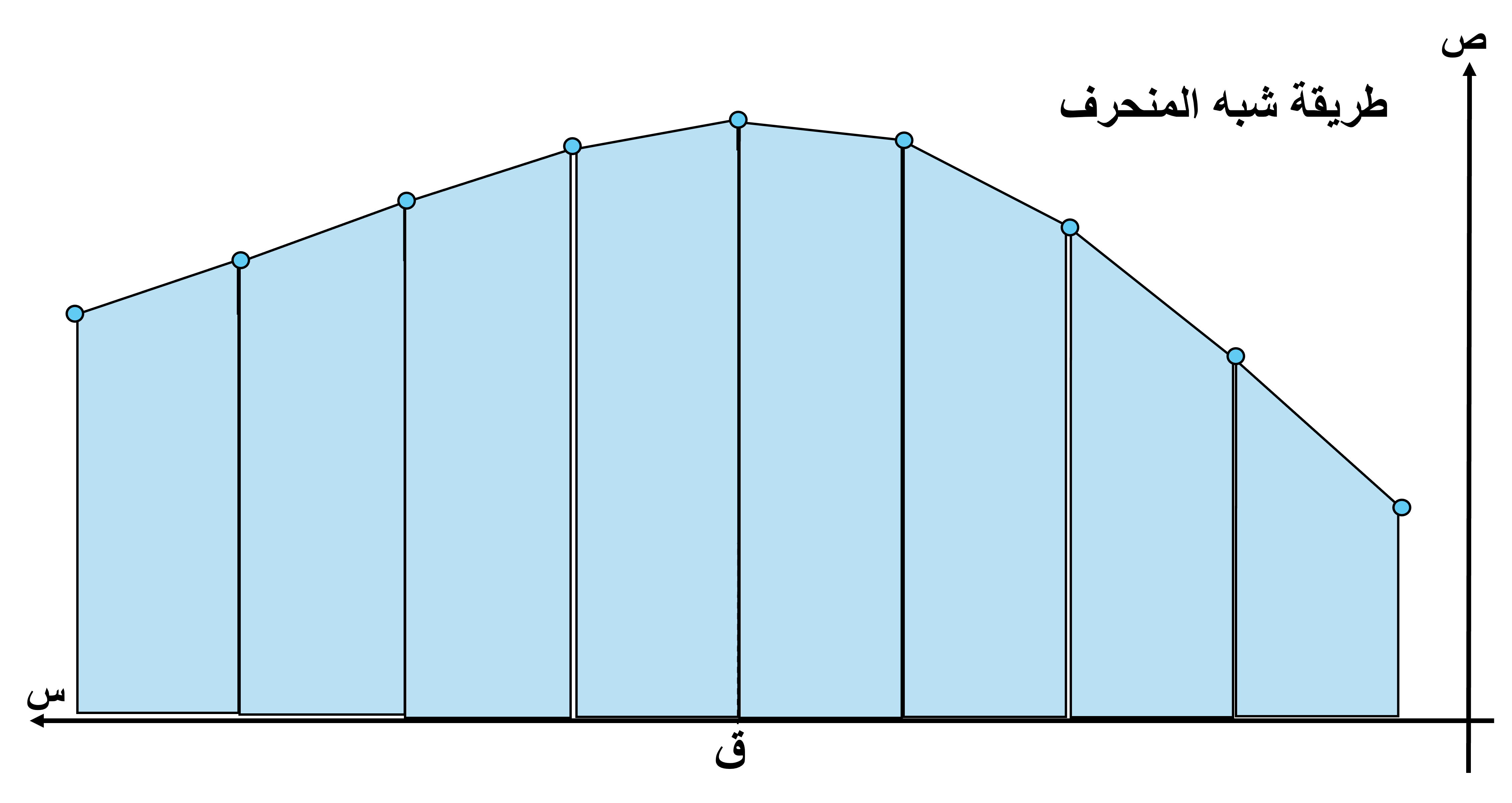
طريقة شبه المنحرف
طريقة شبه المنحرف هي إحدى طرق التكامل العددي، وتُستخدم لتقريب مساحة تحت منحنى دالة عندما لا يمكن حساب التكامل تحليليًا. تعتمد على تقريب الدالة بخطوط مستقيمة بين كل نقطتين متتاليتين، مما يشكّل شكلًا شبه منحرفًا.
تُعتبر طريقة شبه المنحرف أكثر دقة من طريقة المستطيل الأمامي أو الخلفي، وتستخدم على نطاق واسع في التطبيقات العملية.
صيغة طريقة شبه المنحرف
تُحسب المساحة الكلية عن طريق جمع مساحات جميع أشكال شبه المنحرف بين كل زوج من النقاط. الصيغة الأساسية هي:
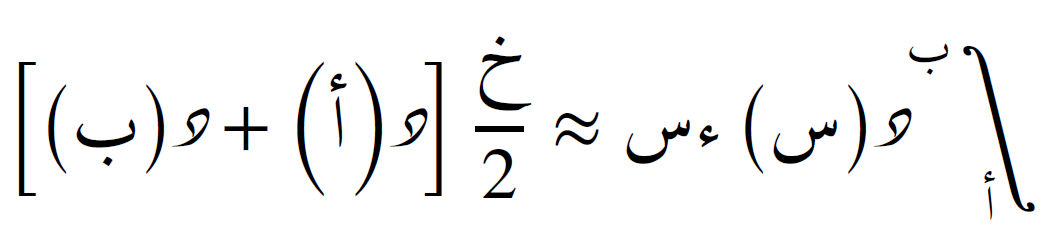
وإذا تم تقسيم الفترة إلى ن فترات فرعية متساوية، فإن الصيغة تصبح:
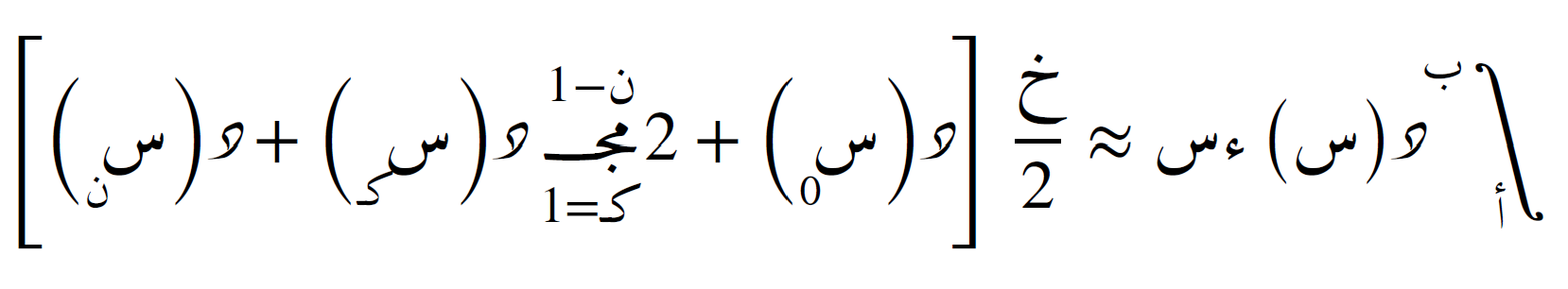
حيث:
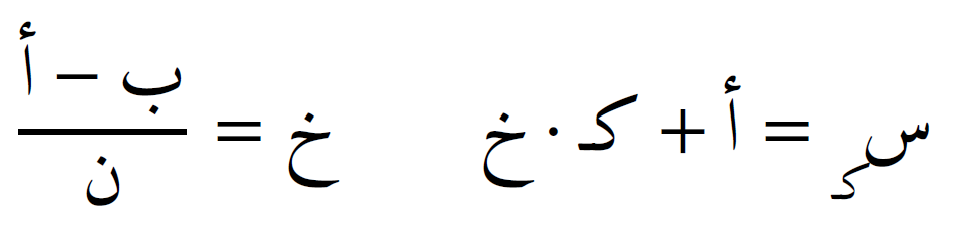
الدقة والخطأ
طريقة شبه المنحرف هي طريقة دقيقة من الرتبة الثانية، وخطأها يتناسب مع ل(خ2)، مما يجعلها أكثر دقة من الطرق المستطيلية.
تُستخدم هذه الطريقة بكثرة عندما تكون الدالة ناعمة.
طريقة الحدوديات: صِيَغ إسحاق
صيغ إسحاق (طريقة الحدوديات) هي إطار عام للتكامل العددي يعتمد على تقريب الدالة عبر كثيرات حدود تمر بمجموعة من النقاط المتساوية التباعد. هذا الإطار يُعمم الطرق الأساسية مثل:
- طريقة المستطيل (الدرجة 0)
- طريقة شبه المنحرف (الدرجة 1)
- طريقة "سمبسون" (الدرجة 2)
- طريقة "سمبسون 3\8" (الدرجة 3)
- طريقة "بوول" (الدرجة 4)
في صيغ طريقة الحدوديات، نقوم بإنشاء تقريب متعدد الحدود كحدن(س) عبر نقاط متساوية التباعد ثم نقوم بتكامل هذا التقريب بدلاً من الدالة الأصلية.:
تشمل النقاط الطرفية للفترة [أ، ب] ضمن الحساب. أي نأخذ القيم عند كل من س0 = أ وسن = ب. هذه الطريقة أكثر شيوعًا وتُستخدم في معظم الحالات.

الصيغة العامة لطريقة الحدوديات
إذا كانت لدينا (ن+1) نقطة متساوية التباعد س0، س1، ... ، سن، فإن الصيغة العامة للتكامل العددي تكون:
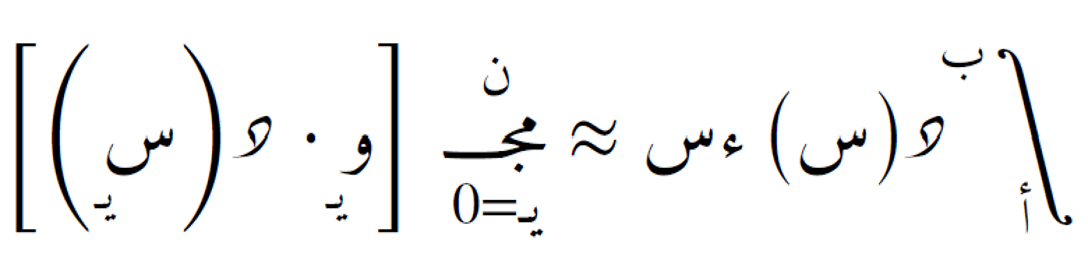
حيث ويـ هي الأوزان المحسوبة من تكامل كثير الحدود المتقطع
الاقتران بواسطة كثيرات الحدود اللاغَرَنجية
نستخدم الاقتران التالي لإنشاء تقريب متعدد الحدود عبر النقاط المعطاة:
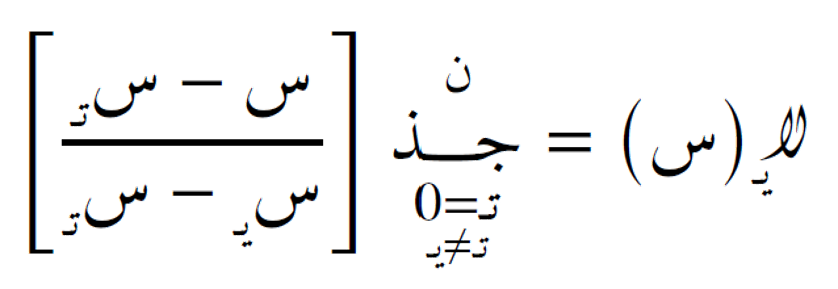
حيث
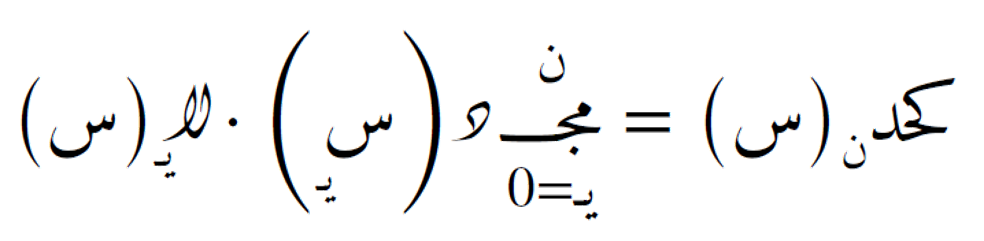
ويُبنى التقريب العام على الشكل:
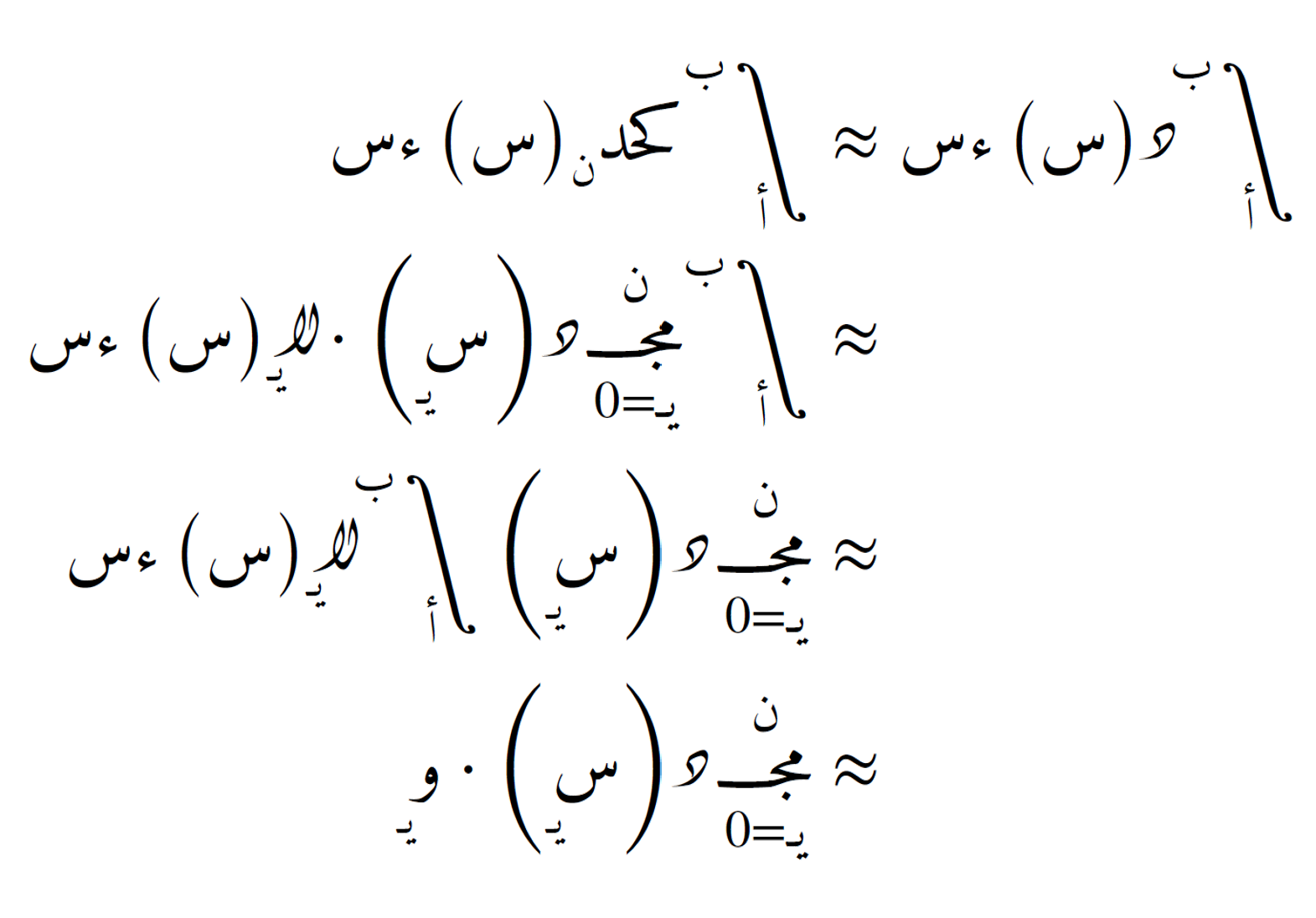
حساب الأوزان
الأوزان هي معاملات تُستخدم في طريقة الحدوديات لتحديد تأثير كل نقطة على التكامل. تُحسب الأوزان بناءً على تكامل كثير الحدود المتقطع.
الدرجة صفر: صيغة المستطيل
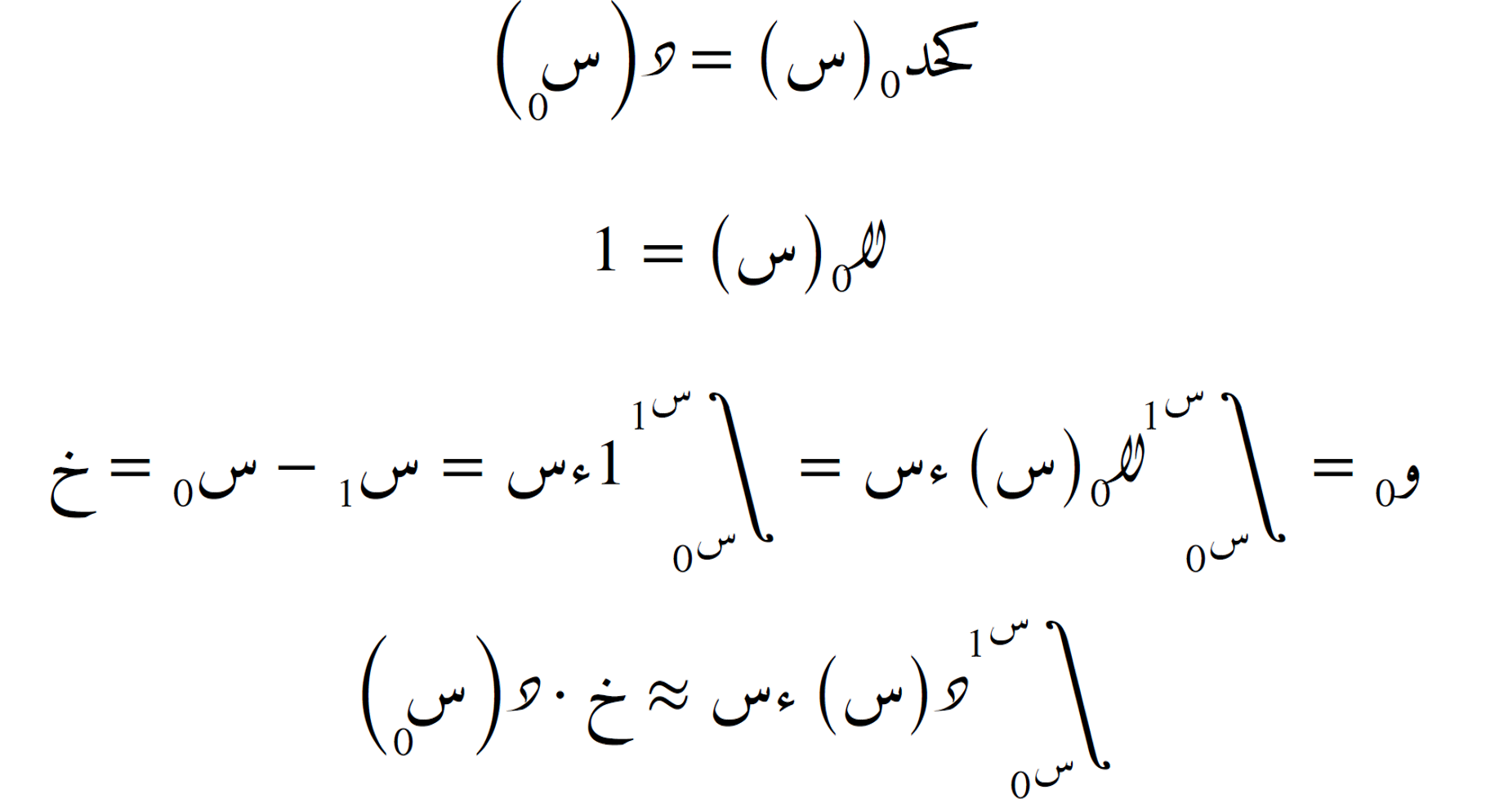
الدرجة الأولى: صيغة شبه المنحرف
نحسب الدوالّ الأساس اللاغَرَنجية كما يلي:
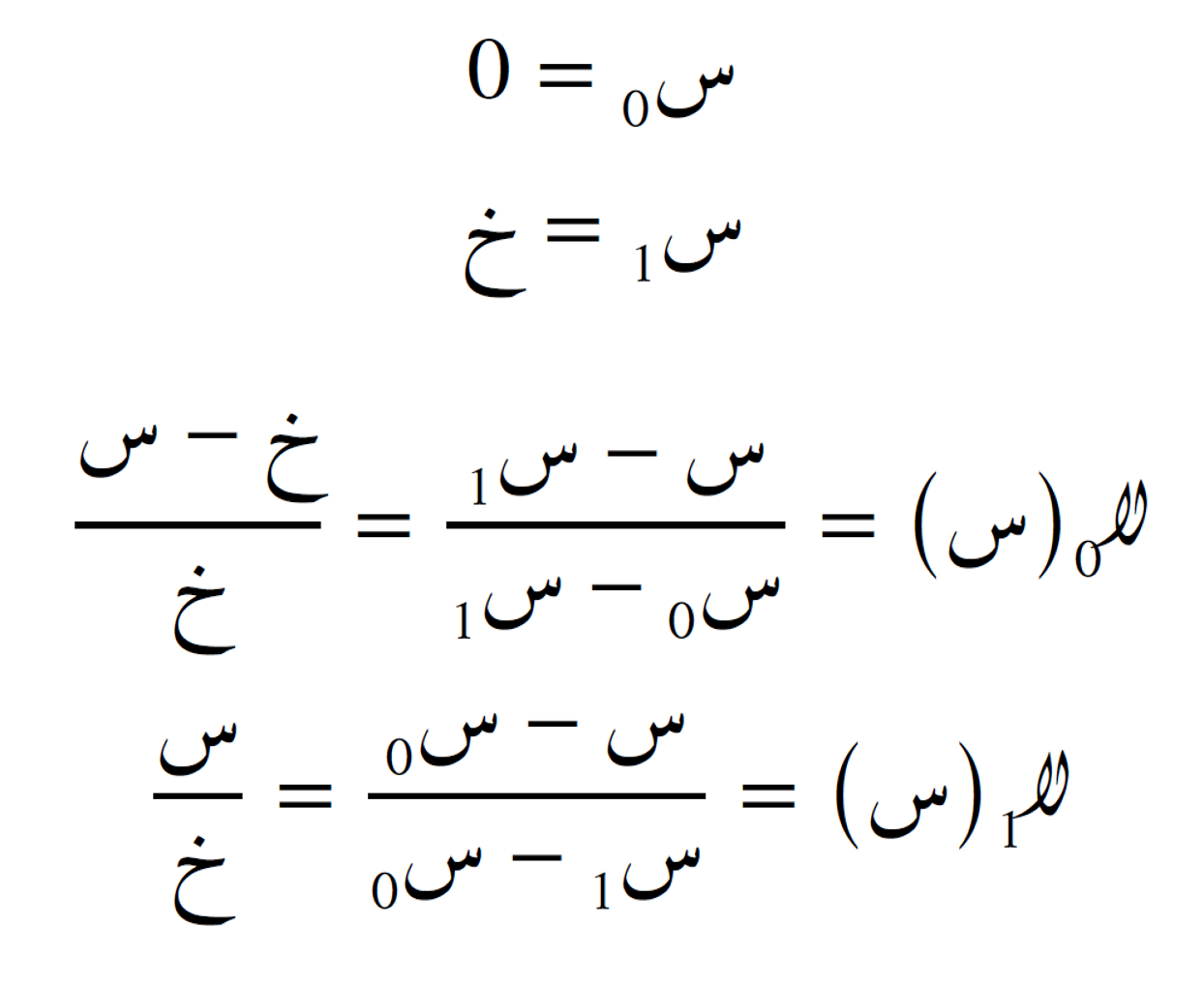
ثم نحسب الأوزان:
وبذلك نحصل على صيغة شبه المنحرف:
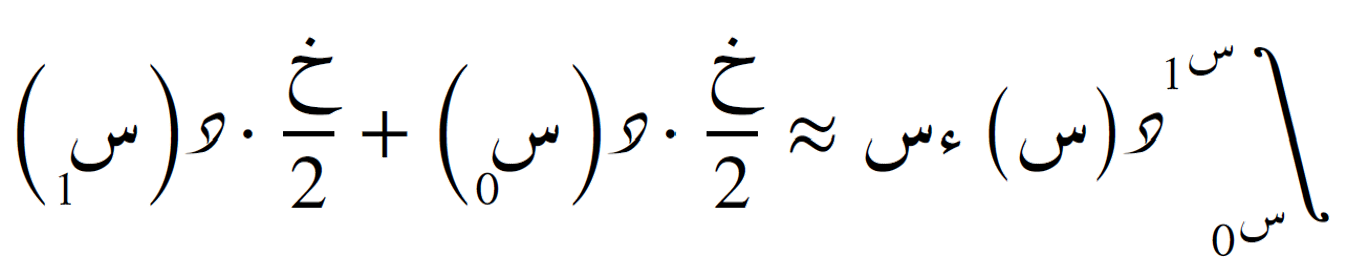
الدرجة الثانية: صيغة سمبسون
نحسب الدوالّ الأساس اللاغَرَنجية كما يلي:
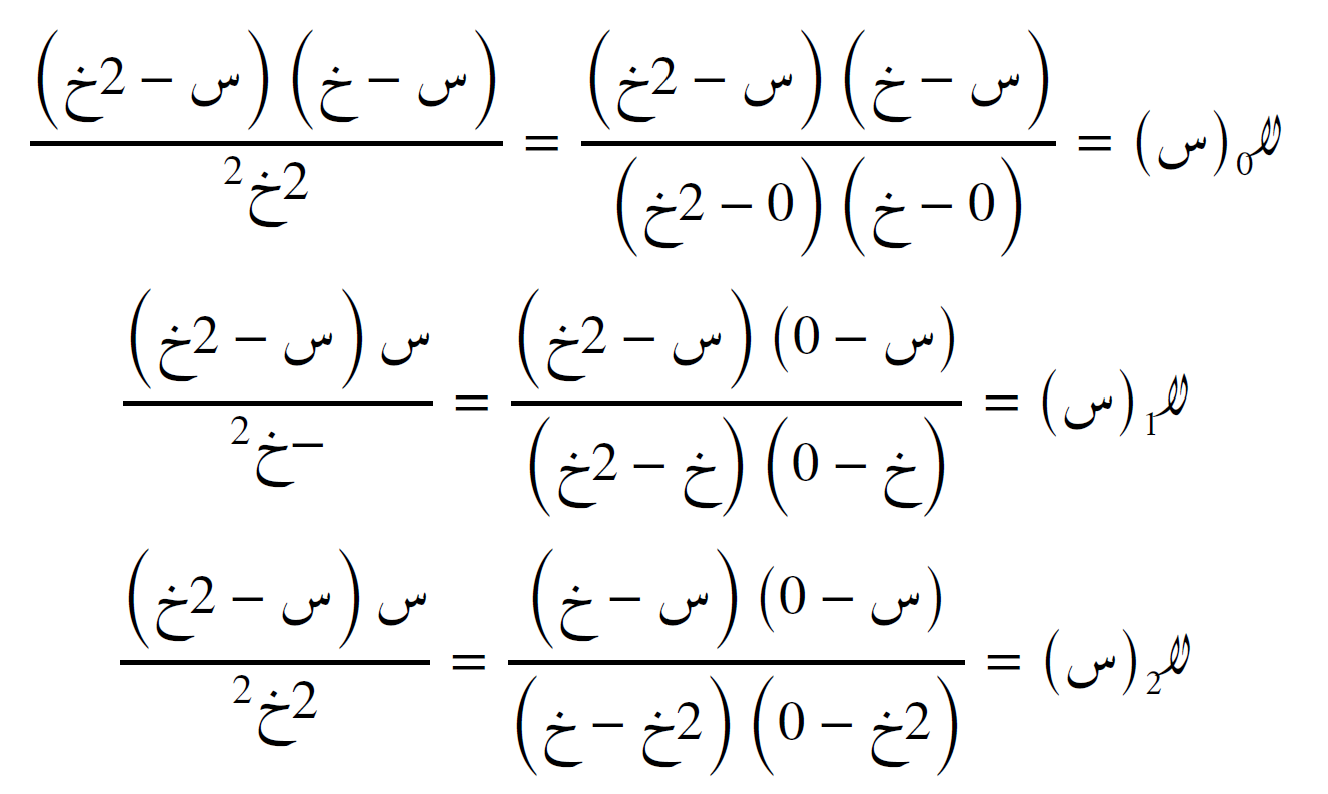
مع
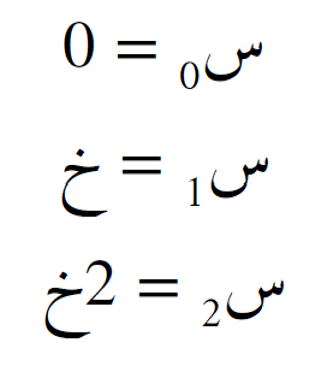
ثم نحسب الأوزان:
وبذلك نحصل على الصيغة من الدرجة الثانية:
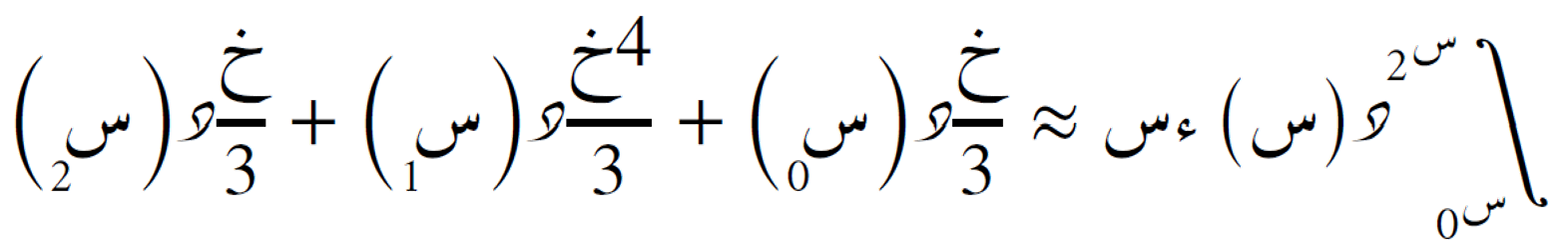
طريقة الحدوديات من الدرجة الثانية
تستخدم ثلاث نقاط متساوية التباعد لتقريب التكامل بواسطة قطع مكافئ (درجة 2). تتطلب أن يكون عدد الفترات زوجيًا.
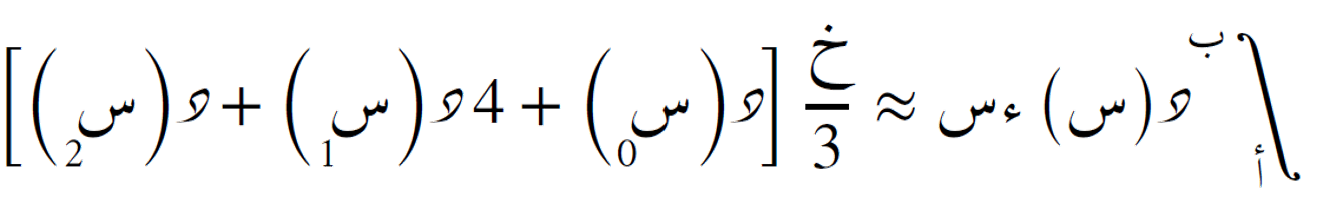
- خ = (ب − أ) ÷ ن
- الدقة: الرتبة الرابعة (تتناسب مع خ4)
- مناسبة عندما يكون ن عددًا زوجيًا
طريقة الحدوديات من الدرجة الثالثة
تمدد لطريقة الدرجة الثانية، تستخدم أربع نقاط (درجة 3) وتناسب الحالات التي يكون فيها عدد الفترات من مضاعفات 3.
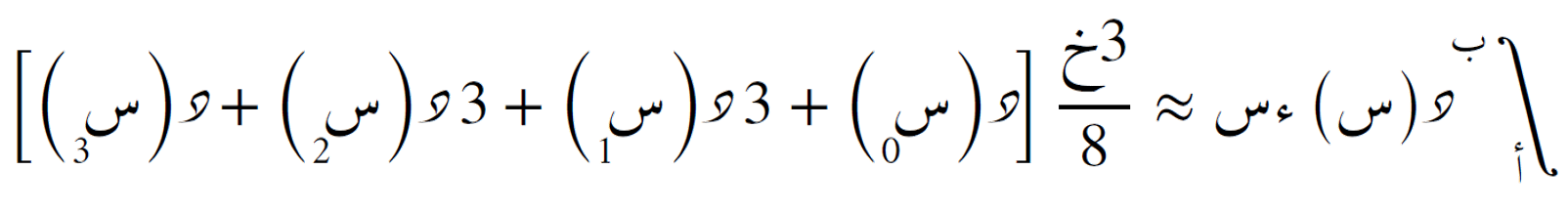
- خ = (ب − أ) ÷ ن ، حيث ن من مضاعفات 3
- الدقة: الرتبة الرابعة (تتناسب مع خ4)
- تستخدم معاملات: 1، 3، 3، 1 (ثم تتكرر)
طريقة الحدوديات من الدرجة الرابعة
طريقة من الدرجة الرابعة (تستخدم خمس نقاط)، وتُوفر دقة أعلى من الطرق السابقة. تُستخدم عندما تكون الدالة ناعمة وتُطلب دقة عالية.
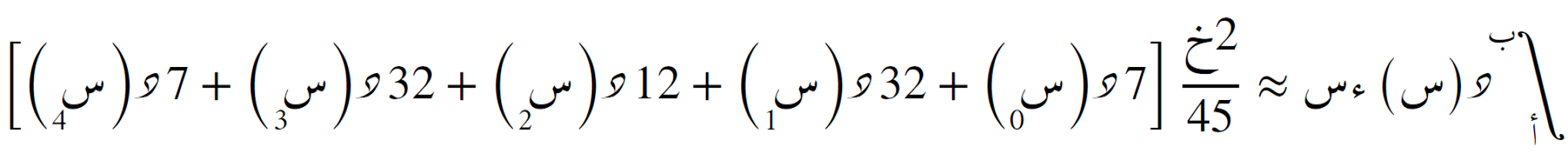
- خ = (ب − أ) ÷ 4
- عدد النقاط: 5
- الدقة: الرتبة السادسة (تتناسب مع خ6)
مقارنة عامة
| الطريقة | درجة التقريب | عدد النقاط | الدقة | الشرط على عدد الفترات |
|---|---|---|---|---|
| المستطيل الأمامي/الخلفي | 0 | 2 | ل(خ) | أي عدد |
| المستطيل المركزي | 1 | 2 | ل(خ2) | أي عدد |
| شبه المنحرف | 1 | 2 | ل(خ2) | أي عدد |
| الحدوديات من الدرجة الثانية | 2 | 3 | ل(خ4) | عدد زوجي |
| الحدوديات من الدرجة الثالثة | 3 | 4 | ل(خ4) | مضاعف لـ 3 |
| الحدوديات من الدرجة الرابعة | 4 | 5 | ل(خ6) | مضاعف لـ 4 (عند التكرار) |
مثال تطبيقي: رسم منحنى مغلق باستخدام المتسلسلة الطيفية التوافقية
من التطبيقات العملية الهامة للتكامل العددي هو تحليل ورسم المنحنيات المغلقة (الكونتور) في المستوى، مثل رسم شكل قلم أو أي مسار مغلق. في هذا المثال، نفترض أن المنحنى مغلق ودوري، ويمكن تمثيله بدوال دورية للموضعين س(ز) وص(ز) حيث ز هو متغير الزمن أو المعلمة التي تتحرك على طول المنحنى.
عند أخذ عينات من نقاط المنحنى (مثلاً من صورة أو رسم)، يمكننا استرجاع الدوال س(ز) وص(ز) باستخدام المتسلسلة الطيفية التوافقية. تعتمد هذه الطريقة على أن كل من س وص يمكن تمثيلهما كمجموع من الدوال الجيبية وجيب التمام بترددات مختلفة.
لحساب معاملات الطيف من النقاط المأخوذة، نحتاج إلى حساب تكاملات عددية (مجموعات) على القيم المأخوذة عند كل نقطة. هنا تظهر أهمية التكامل العددي، حيث تُستخدم طرق مثل شبه المنحرف أو سمبسون لتقريب هذه التكاملات بدقة من القيم المنفصلة.
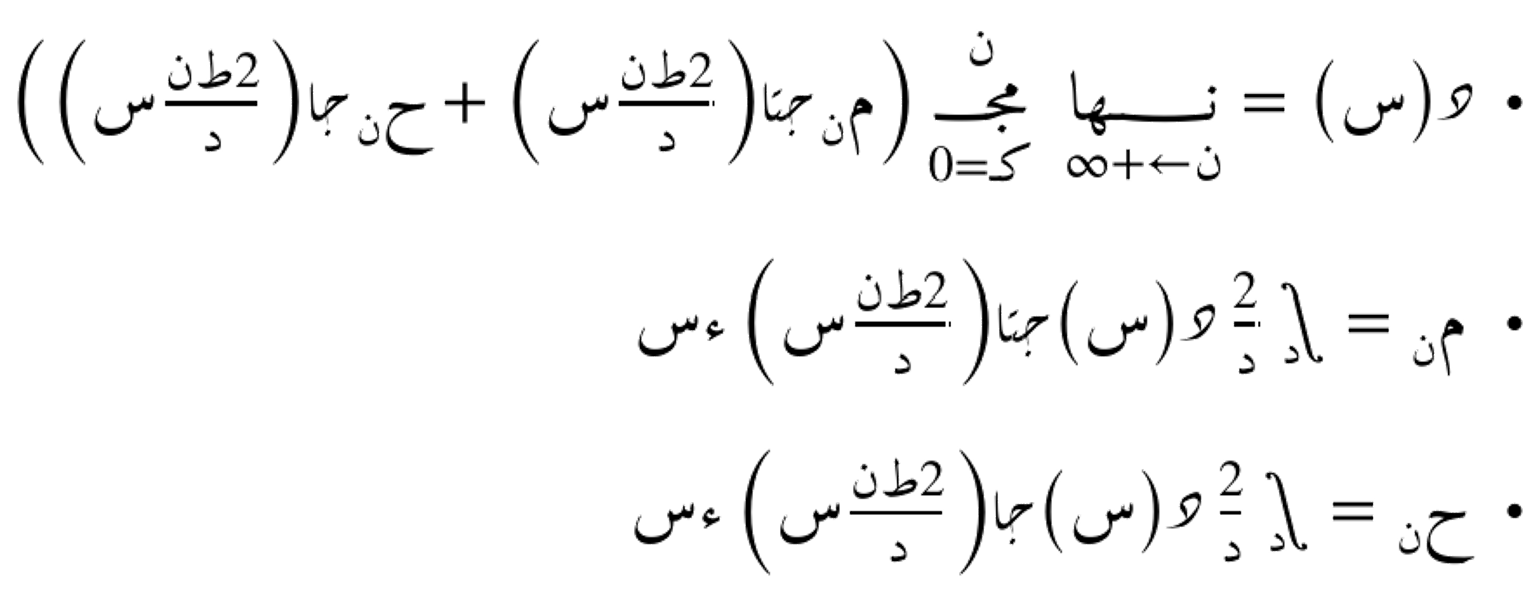
مع د هو مُدّة أو طول الدورة المُعتبرة و هيَ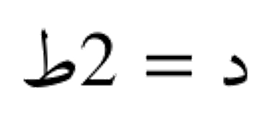
في الصورة أعلاه، نرى الشكل الأصلي للمنحنى المغلق الذي نريد تحليله.
هنا تم أخذ عينات من نقاط المنحنى بشكل دوري(حوالي خمسون وسِتة مائة نقطة). هذه النقاط هي ما سنستخدمه لاستخلاص معاملات الطيف. نختار أيضا طريقة التكامل الرقمي بشبه المنحرف لحساب التكاملات اللازمة.
في هذا السياق، ن هو عدد التوافقيات (عدد حدود المتسلسلة الطيفية التوافقية). كلما زاد عدد التوافقيات المستخدمة، زادت دقة تقريب المنحنى الأصلي بواسطة المتسلسلة الطيفية التوافقية. في الرسوم المتحركة أعلاه، نلاحظ كيف يتحسن التقريب مع زيادة عدد التوافقيات.
تمثيل المنحنى وتحليل الإحداثيات
بعد حساب معاملات الطيف لكل من س(ز) وص(ز)، يمكننا إعادة رسم المنحنى الأصلي بدقة عالية. يُظهر الشكل التالي كيف يتم تتبع المنحنى في المستوى باستخدام هذه المعاملات:
كما يمكن تحليل كل من الإحداثيين س(ز) وص(ز) على حدة كدوال دورية بالنسبة للمعلمة ز:
في المخططات أعلاه، نلاحظ كيف تتغير قيم س وص مع تغير ز بشكل دوري. هذه الدوال الدورية هي التي يتم تحليلها بواسطة المتسلسلة الطيفية التوافقية، وتُحسب معاملات الطيف لها باستخدام التكامل العددي على النقاط المأخوذة من المنحنى.
تأمل رياضي: من المدهش أن من يرى الرسوم البيانية للإحداثيين س وص منفصلين، لن يخطر بباله أبداً أن الشكل الناتج في المستوى هو كلمة "الله" بخط عربي جميل.
سبحان الله، كيف أن الرياضيات تمنحنا أدوات لفهم الأنماط الخفية والجمال الكامن في الكون، وتُذكرنا بعظمة الخالق في إبداع النظام والدقة حتى في أبسط النقاط والمنحنيات. إن التأمل في هذه النتائج يفتح لنا باب التفكر في قدرة الله وحكمته في خلقه، ويجعلنا نرى الرياضيات وسيلة للتدبر في آيات الله في الآفاق والأنفس.











