التكامل الرقمي

تُستخدم صيغ إسحاق متعددة الأبعاد لتقريب التكاملات في الفضاءات ذات الأبعاد الأعلى مثل ح² أو ح³، وتُبنى من صيغ إسحاق الأحادية عبر جداء مُوَتري.

يعتمد هذا الأسلوب على تطبيق صيغة أحادية البُعد على كل بُعد على حدة، ثم ضرب النتائج معًا، مما يعطي تقديرًا للتكامل المتعدد.

✦الصيغة العامة (جداء مُوَتري ثنائي الأبعاد)

إذا كانت لدينا دالة \( د(س, ص) \) على المجال المستطيل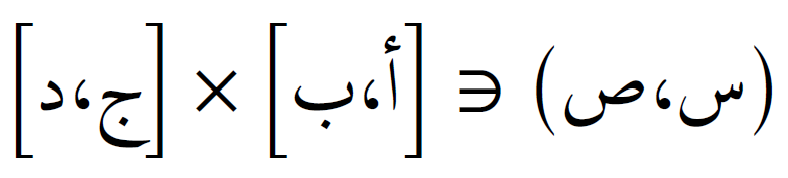، فإن التكامل يُقرب على الشكل:

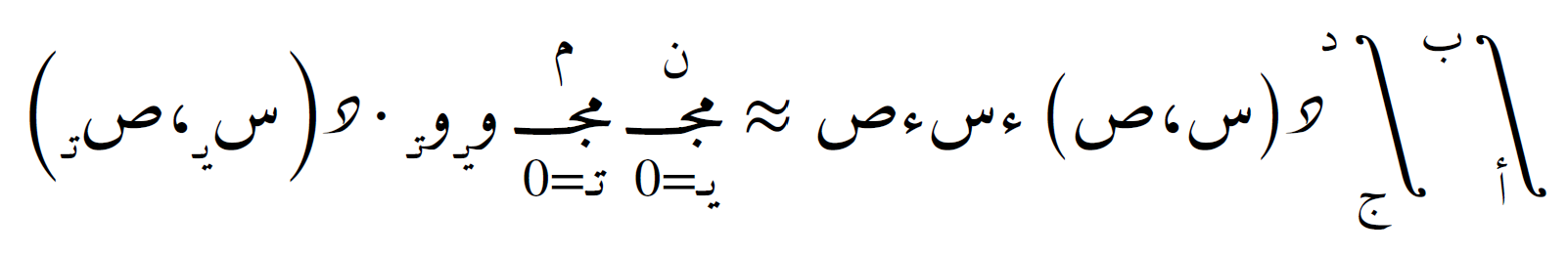
ويمكن تعميم هذا إلى أبعاد أعلى، باستخدام مجموعات مزدوجة أو ثلاثية من الأوزان والنقاط لكل بُعد.

✦1. قاعدة المستطيل (الدرجة 0)

تُستخدم القيمة في الزاوية اليسرى السفلية من كل خلية في الشبكة لحساب الحجم التقديري. الصيغة الثنائية البُعد هي:

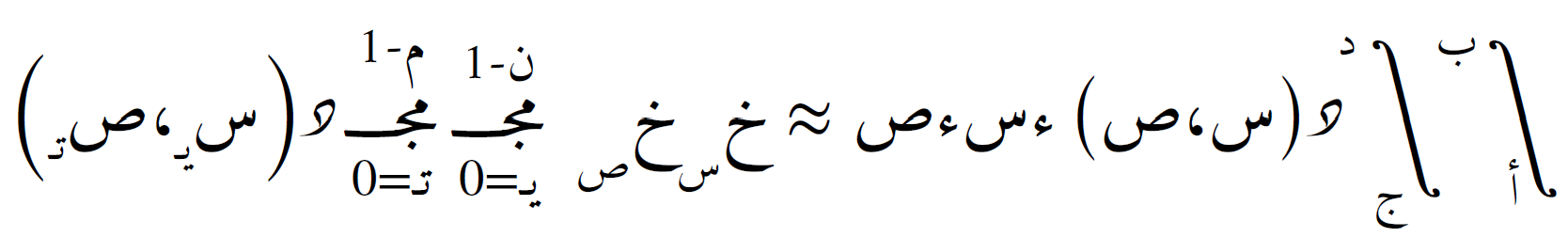
حيث:

✦2. قاعدة شبه المنحرف (الدرجة 1)

يتم تطبيق قاعدة شبه المنحرف في كل بعد، ثم تُدمج النتائج. الصيغة الثنائية البُعد تأخذ الشكل:

حيث مُعاملي س و ص:

في هذا التقدير، يتم استخدام أوزان مختلفة عند الحدود والزوايا لتقليل الخطأ.

✦3. قاعدة سمبسون 1\3 (الدرجة 2)

يمكن أيضًا تعميم قاعدة "سمبسون" ثنائية البُعد باستخدام الجداء المُوَتري:

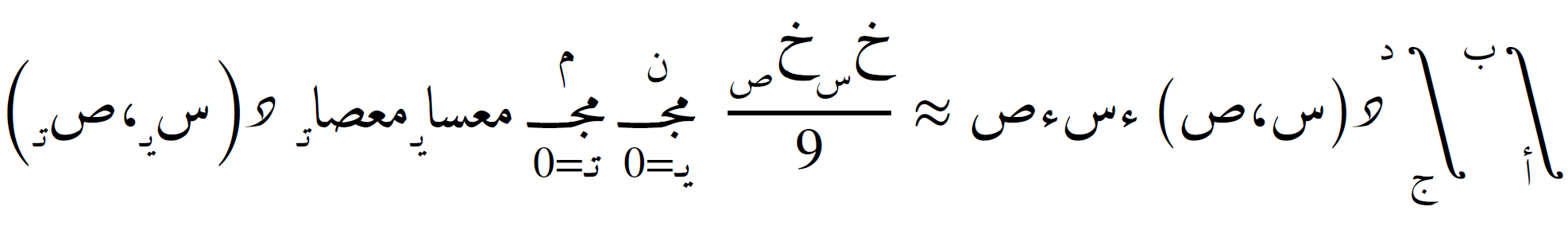
حيث مُعاملي س و ص:

يجب أن يكون عدد الفترات في كل بُعد زوجيًا. ويُستخدم التكرار بين الأوزان 1 و4 و2 في كلا البُعدين.

✦مزايا التكامل المُوَتري متعدد الأبعاد

• سهل التنفيذ: باستخدام صيغ أحادية مكررة
• يتناسب مع الشبكات المنتظمة: مفيد في التطبيقات الشبكية
• عيب:عدد نقاط العينة ينمو أُسّيًا مع الأبعاد

✦متى نستخدم التكامل المُوَتري؟

• عند توفر الدالة كقيمة عددية على شبكة منتظمة
• عند تنفيذ تكاملات عددية في محاكاة فيزيائية أو هندسية
• عند الرغبة في زيادة الدقة تدريجيًا حسب الحاجة

✦الصيغة العامة في الأبعاد النونية

يمكن تعميم التكامل إلى الدوالّ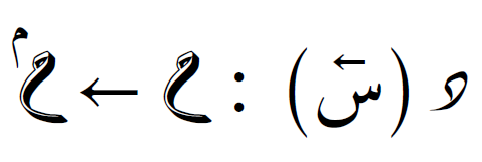كما يلي، حيث يُستخدم الجداء المُوَتري على جميع الأبعاد:

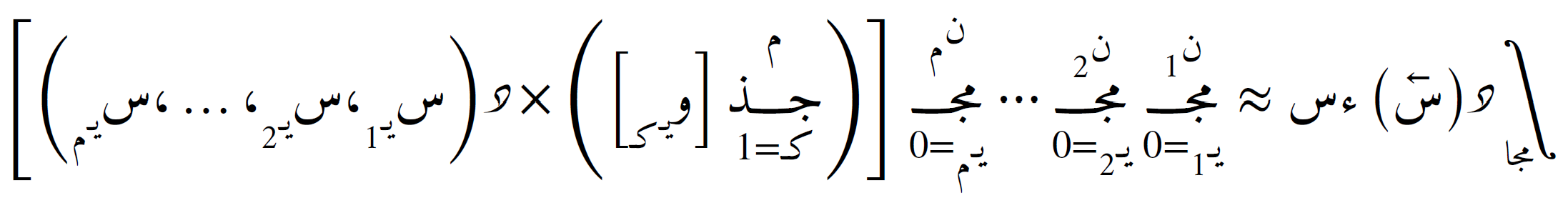
مع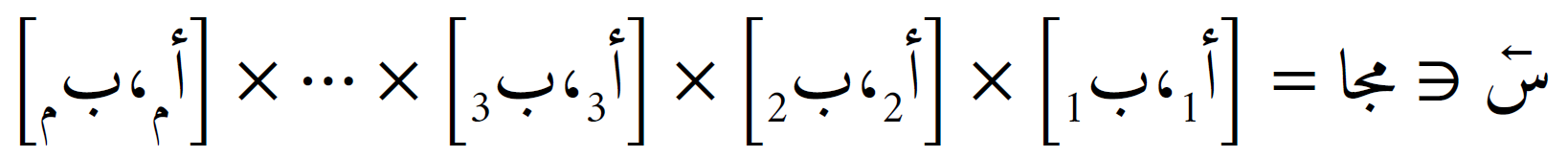

هذه الصيغة تعبّر عن جمع القيم على شبكة منتظمة باستخدام أوزان مأخوذة من القواعد الأحادية، وتُستخدم بكفاءة في التكامل العددي متعدد الأبعاد في التطبيقات المتقدمة.